Caratteristiche e proprietà dei vettori, elementi, tipi, esempi

Il vettore Sono entità matematiche che hanno una grandezza -positiva-, generalmente accompagnata da un'unità di misura, oltre che da direzione e senso. Tali caratteristiche sono molto appropriate per descrivere grandezze fisiche come velocità, forza, accelerazione e molte altre..

Con i vettori è possibile eseguire operazioni come addizioni, sottrazioni e prodotti. La divisione non è definita per i vettori e per quanto riguarda il prodotto, ci sono tre classi che descriveremo in seguito: prodotto scalare o punto, prodotto vettoriale o croce e prodotto di uno scalare per un vettore.

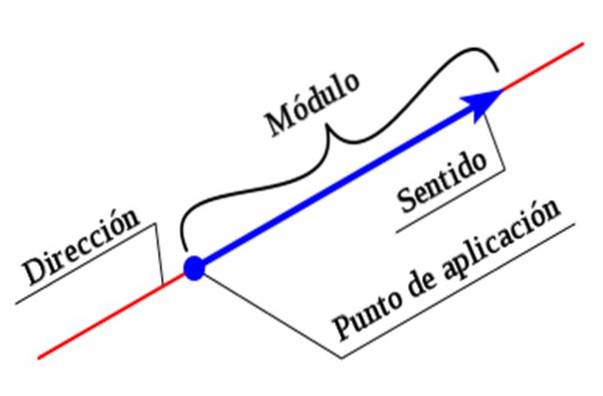
Per descrivere completamente un vettore, è necessario indicare tutte le sue caratteristiche. La grandezza o modulo è un valore numerico accompagnato da un'unità, mentre la direzione e la direzione sono stabilite con l'aiuto di un sistema di coordinate.

Facciamo un esempio: diciamo che un aereo vola da una città all'altra a una velocità di 850 km / h in direzione NE. Qui abbiamo un vettore completamente specificato, poiché la magnitudine è disponibile: 850 km / h, mentre la direzione e il senso sono NE.

I vettori sono solitamente rappresentati graficamente da segmenti di linea orientati, la cui lunghezza è proporzionale alla grandezza.

Mentre per specificare la direzione e il senso è necessaria una linea di riferimento, che di solito è l'asse orizzontale, sebbene si possa prendere come riferimento anche il nord, tale è il caso della velocità del piano:

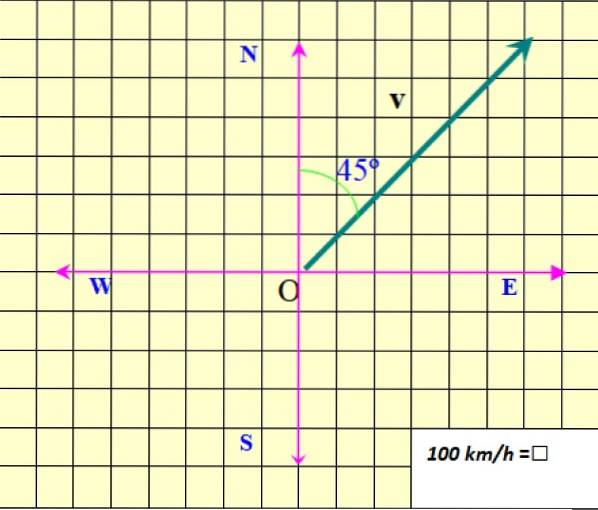
La figura mostra il vettore velocità del piano, che è indicato come v sopra grassetto, per distinguerlo da una quantità scalare, che richiede solo un valore numerico e qualche unità da specificare.

Indice articolo

• 1 Elementi di un vettore
  • 1.1 Componenti rettangolari di un vettore
• 2 tipi
  • 2.1 Vettori unità ortogonali
• 3 Somma di vettori
  • 3.1 Proprietà dell'addizione di vettori
• 4 esempi vettoriali
• 5 Altre operazioni tra vettori
  • 5.1 Prodotto di uno scalare e di un vettore
  • 5.2 Prodotto scalare o prodotto scalare tra vettori
  • 5.3 Prodotto incrociato o prodotto incrociato tra vettori
• 6 Esercizi risolti
  • 6.1 - Esercizio 1
  • 6.2 - Esercizio 2
• 7 Riferimenti

Elementi di un vettore

Come abbiamo detto, gli elementi del vettore sono:

-Magnitudine o modulo, a volte chiamato anche valore assoluto o norma del vettore.

-Direzione

-Senso

Nell'esempio in figura 2, il modulo v È 850 km / h. Il modulo è indicato come v senza grassetto o come |v|, dove le barre rappresentano il valore assoluto.

L'indirizzo di v è specificato rispetto al Nord. In questo caso è 45º Nord Est (45º NE). Infine la punta della freccia informa sulla direzione di v.

In questo esempio, l'origine del vettore è stata disegnata in coincidenza con l'origine O del sistema di coordinate, questo è noto come vettore legato. Se invece l'origine del vettore non coincide con quella del sistema di riferimento si dice che sia un vettore gratuito.

Va notato che per specificare completamente il vettore, questi tre elementi devono essere annotati, altrimenti la descrizione del vettore sarebbe incompleta.

Componenti rettangolari di un vettore

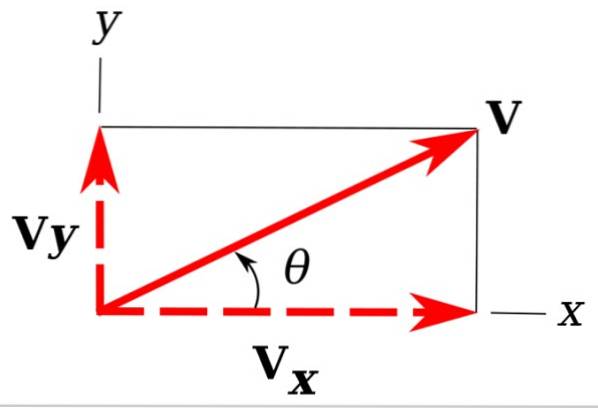
Nell'immagine abbiamo il nostro vettore di esempio indietro v, quello è nell'aereo xy.

È facile vedere che le proiezioni di v sugli assi delle coordinate xey determinano un triangolo rettangolo. Queste proiezioni lo sono v_Y Y v_X e sono chiamati componenti rettangolari di v.

Un modo per denotare v attraverso le sue componenti rettangolari è così: v = X, v_Y>. Queste parentesi vengono utilizzate al posto delle parentesi per sottolineare il fatto che si tratta di un vettore e non di un punto, poiché in questo caso verrebbero utilizzate le parentesi.

Se il vettore è nello spazio tridimensionale, è necessario un altro componente, in modo che:

v = X, v_Y, v_z>

Conoscendo le componenti rettangolari, si calcola la grandezza del vettore, equivalente a trovare l'ipotenusa del triangolo rettangolo le cui gambe sono v_X Y v_Y,. Per mezzo del teorema di Pitagora segue che:

|v|^Due = (v_X)^Due +  (v_Y)^Due

Forma polare di un vettore

Quando la grandezza del vettore è nota |v| e l'angolo θ che questo forma con l'asse di riferimento, generalmente l'asse orizzontale, è anche specificato il vettore. Si dice quindi che il vettore è espresso in forma polare.

I componenti rettangolari in questo caso sono facilmente calcolabili:

v_X = |v| .cos θ

v_Y = |v| .sen θ

Secondo quanto sopra, le componenti rettangolari del vettore velocità v dell'aereo sarebbe:

v_X = 850. cos 45º km / h = 601,04 km / h

v_Y = 850. sin 45º km / h = 601,04 km / h

Tipi

Esistono diversi tipi di vettori. Esistono vettori di velocità, posizione, spostamento, forza, campo elettrico, quantità di moto e molti altri. Come abbiamo già detto, in fisica ci sono un gran numero di quantità vettoriali.

Per quanto riguarda i vettori che hanno determinate caratteristiche, possiamo menzionare i seguenti tipi di vettori:

-Nullo: questi sono vettori la cui grandezza è 0 e che sono indicati come 0. Ricorda che la lettera in grassetto simboleggia le tre caratteristiche fondamentali di un vettore, mentre la lettera normale rappresenta solo il modulo.

Ad esempio, su un corpo in equilibrio statico, la somma delle forze deve essere un vettore nullo.

-Libero e vincolato: i vettori liberi sono quelli i cui punti di origine e di arrivo sono una qualsiasi coppia di punti nel piano o nello spazio, a differenza dei vettori collegati, la cui origine coincide con quella del sistema di riferimento utilizzato per descriverli.

La coppia o il momento prodotto da una coppia di forze è un buon esempio di vettore libero, poiché la coppia non si applica a nessun punto particolare.

-Obiettivi di squadra: sono due vettori liberi che condividono caratteristiche identiche. Pertanto hanno uguale grandezza, direzione e senso.

-Complanare o complanare: vettori che appartengono allo stesso piano.

-Opposti: vettori di uguale grandezza e direzione, ma direzioni opposte. Il vettore opposto a un vettore v è il vettore -v e la somma di entrambi è il vettore nullo: v + (-v) = 0.

-Concorrente: vettori le cui linee di azione passano tutte per lo stesso punto.

-Sliders: sono quei vettori il cui punto di applicazione può scorrere lungo una linea particolare.

-Collineare: vettori che si trovano sulla stessa linea.

-Unitario: quei vettori il cui modulo è 1.

Vettori di unità ortogonali

Esiste un tipo di vettore molto utile in fisica chiamato vettore unità ortogonale. Il vettore unità ortogonale ha un modulo uguale a 1 e le unità possono essere qualsiasi, ad esempio quelle di velocità, posizione, forza o altre.

Esiste un insieme di vettori speciali che aiutano a rappresentare facilmente altri vettori e ad eseguire operazioni su di essi: sono vettori unità ortogonali io, j Y K, unitari e perpendicolari tra loro.

In due dimensioni, questi vettori sono diretti lungo la direzione positiva di entrambi gli assi X a partire dall'asse Y. E in tre dimensioni viene aggiunto un vettore unitario nella direzione dell'asse z positivo. Sono rappresentati come segue:

io = <1, 0,0>

j = < 0,1,0>

K = <0,0,1>

Un vettore può essere rappresentato dai vettori unitari io, j Y K come segue:

v = v_X io + v_Y j + v_z K

Ad esempio il vettore velocità v dagli esempi precedenti può essere scritto come:

v = 601,04 io + 601.04 j km / h

Il componente in K non è necessario, poiché questo vettore è nel piano.

Aggiunta di vettore

La somma dei vettori appare molto frequentemente in varie situazioni, ad esempio quando si desidera trovare la forza risultante su un oggetto che è influenzato da varie forze. Per iniziare, supponiamo di avere due vettori liberi o Y v sull'aereo, come mostrato nella figura seguente a sinistra:

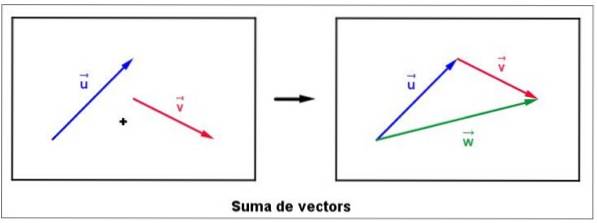
Viene immediatamente spostato con attenzione nel vettore v, senza modificarne l'ampiezza, la direzione o il senso, in modo che la sua origine coincida con la fine di o.

Viene chiamato il vettore somma w ed è disegnato a partire da u che termina con v, secondo la figura a destra. È importante notare che la grandezza del vettore w non è necessariamente la somma delle grandezze di v Y o.

Se ci pensi attentamente, l'unica volta in cui la grandezza del vettore risultante è la somma delle grandezze degli addendi, è quando entrambi gli addendi sono nella stessa direzione e hanno lo stesso senso..

E cosa succede se i vettori non sono liberi? È anche molto facile aggiungerli. Il modo per farlo è aggiungere componente a componente o metodo analitico.

A titolo di esempio, consideriamo i vettori nella figura seguente, la prima cosa è esprimerli in uno dei modi cartesiani precedentemente spiegati:

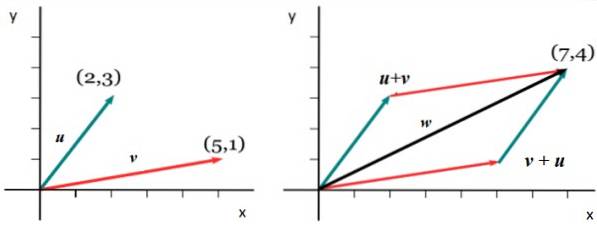
v = <5,1>

o = <2,3>

Per inserire il componente X del vettore somma w, i rispettivi componenti vengono aggiunti X a partire dal v Y o: w_X = 5 + 2 = 7. E per ottenere w_Y si segue una procedura analoga: w_Y = 1 + 3. Perciò:

o = <7,4>

Proprietà dell'addizione di vettori

-La somma di due o più vettori produce un altro vettore.

-È commutativo, l'ordine degli addendi non altera la somma, in modo tale che:

o + v = v + o

-L'elemento neutro della somma dei vettori è il vettore nullo: v + 0 = v

-La sottrazione di due vettori è definita come la somma del contrario: v - u = v + (-o)

Esempi vettoriali

Come abbiamo detto, esistono numerose quantità vettoriali in fisica. Tra i più noti ci sono:

-Posizione

-Dislocamento

-Velocità media e velocità istantanea

-Accelerazione

-Vigore

-Quantità di movimento

-Coppia o momento di una forza

-Impulso

-campo elettrico

-Campo magnetico

-Momento magnetico

D'altra parte, non sono vettori ma scalari:

-Tempo metereologico

-Massa

-Temperatura

-Volume

-Densità

-Lavoro meccanico

-Energia

-Caldo

-Energia

-Voltaggio

-Corrente elettrica

Altre operazioni tra vettori

Oltre all'addizione e alla sottrazione di vettori, ci sono altre tre operazioni molto importanti tra i vettori, perché danno origine a nuove quantità fisiche molto importanti:

-Prodotto di uno scalare e di un vettore.

-Il prodotto scalare o il prodotto scalare tra i vettori

-E il prodotto incrociato o vettoriale tra due vettori.

Prodotto di uno scalare e di un vettore

Considera la seconda legge di Newton, che afferma che la forza F e accelerazione per sono proporzionali. La costante di proporzionalità è la massa m dell'oggetto, quindi:

F = m.per

La massa è uno scalare; forza e accelerazione sono vettori. Poiché la forza si ottiene moltiplicando la massa per l'accelerazione, è il risultato del prodotto di uno scalare e di un vettore.

Questo tipo di prodotto risulta sempre in un vettore. Ecco un altro esempio: la quantità di movimento. Essere P il vettore della quantità di moto, v il vettore di velocità e come sempre, m è la massa:

P = m.v

Prodotto a punti o prodotto a punti tra vettori

Abbiamo inserito il lavoro meccanico nell'elenco delle quantità che non sono vettori. Tuttavia, il lavoro in fisica è il risultato di un'operazione tra vettori chiamata prodotto scalare, prodotto interno o prodotto scalare..

Lascia che siano i vettori v Y o, il prodotto scalare o scalare tra di loro è definito come:

v∙o = |v| ∙ |o | .cos θ

Dove θ è l'angolo tra i due. Dall'equazione mostrata segue immediatamente che il risultato del prodotto scalare è uno scalare e anche che se entrambi i vettori sono perpendicolari, il loro prodotto scalare è 0.

Torna al lavoro meccanico W, questo è il prodotto scalare tra il vettore forza F e il vettore di spostamento ℓ.

W = F∙ℓ                  

Quando i vettori sono disponibili in termini di componenti, anche il prodotto scalare è molto facile da calcolare. sì v = X, v_Y, v_z > Y o = X, o_Y, o_z >, il prodotto scalare tra i due è:

v∙o = v_X o_X + v_Y o_Y + v_z o_z

Il prodotto scalare tra i vettori è commutativo, quindi:

v∙o = o∙v

Prodotto incrociato o prodotto vettoriale tra vettori

sì v e tu sei i nostri due vettori di esempio, il prodotto vettoriale è definito come:

v X o = w

Ne consegue immediatamente che il prodotto incrociato risulta in un vettore, il cui modulo è definito come:

|v X u | = | v | . | u |. sen θ

Dove θ è l'angolo tra i vettori.

Il prodotto incrociato non è quindi commutativo v X u ≠ u X v. Infatti v X u = - (u X v).

Se i due vettori di esempio sono espressi in termini di vettori unitari, il calcolo del prodotto vettoriale è più semplice:

v = v_X io + v_Y j + v_z K

o = u_X io + o_Y j + o_z K

Prodotti incrociati tra vettori unitari

Il prodotto incrociato tra vettori unitari identici è zero, poiché l'angolo tra loro è 0º. Ma tra diversi vettori unitari, l'angolo tra di loro è 90º e sin 90º = 1.

Il diagramma seguente aiuta a trovare questi prodotti. Nella direzione della freccia ha una direzione positiva e nella direzione opposta ha una direzione negativa:

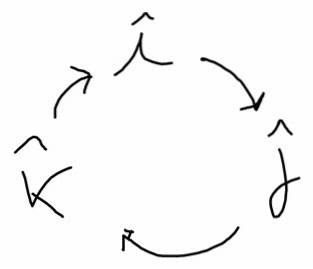
io X j = k, j X K = io; K X io = j; j X i = -k; K X j = -io; io X K = -j

Applicando la proprietà distributiva, che è ancora valida per i prodotti tra vettori più le proprietà dei vettori unitari, abbiamo:

v X o = (v_X io + v_Y j + v_z K) x (u_X io + o_Y j + o_z K) =  

= (v_Yo_z - v_zo_Y )io + (v_zo_X - v_Xo_z )j + (v_Xo_Y - v_Yo_X )K

Esercizi risolti

- Esercizio 1

Dati i vettori:

v = -5 io + 4j + 1 K

o = 2 io -3 j + 7K

Quale dovrebbe essere il vettore w in modo che la somma v + o + w si scopre 6 io +8 j -10K?

Soluzione

-5 io + 4j + 1 K

Due io -3 j + 7K

 w_X io + w_Y j + w_z K  +

--

6io + 8 j -10 K

Pertanto, è necessario soddisfare che:

-5 +2 + sett_X = 6 → w_X = 9

4-3 + w_Y = 8 → w_Y = 7

1 + 7 + w_z = -10 → w_z = -18

La risposta è: w = 9 io +7 j - 18K

- Esercizio 2

Qual è l'angolo tra i vettori v Y o dall'esercizio 1?

Soluzione

Useremo il prodotto dot. Dalla definizione abbiamo:

cos θ = v∙o / |v| ∙ |o|

v∙o= -10-12 + 7 = -15

|v| = √ (-5)^Due +4^Due +1^Due= √42 = 6,48

|o| = √2^Due +(-3)^Due +7^Due= √62 = 7,87

Sostituendo questi valori:

cos θ = -15 / 6,48 x 7,87 = -0,2941 → θ = 107,1 º

Riferimenti

1. Figueroa, D. (2005). Serie: Fisica per la scienza e l'ingegneria. Volume 1. Cinematica. A cura di Douglas Figueroa (USB).
2. Giancoli, D. 2006. Fisica: principi con applicazioni. 6 °. Ed prentice hall.
3. Rex, A. 2011. Fondamenti di fisica. Pearson.
4. Sears, Zemansky. 2016. Fisica universitaria con fisica moderna. 14th. Ed. Volume 1.
5. Serway, R., Jewett, J. 2008. Fisica per la scienza e l'ingegneria. Volume 1. 7th. Ed. Cengage Learning.