
Caratteristiche ed esempi delle variabili categoriali

Il variabile categoriale È quello utilizzato in statistica per assegnare una caratteristica o una proprietà non numerica o qualitativa a un oggetto, individuo, entità, condizione o procedura. È possibile definire tutti i tipi di variabili categoriali in base a ciascuna esigenza.
Esempi di variabili categoriali sono: colore, sesso, gruppo sanguigno, stato civile, tipo di materiale, forma di pagamento o tipo di conto bancario e sono molto utilizzati su base giornaliera..

Quelle sopra sono le variabili, ma i loro possibili valori sono qualitativi, cioè di qualità o caratteristici e non di misura numerica. Ad esempio i possibili valori per la variabile sesso Sono: maschio , hembra.
Quando questa variabile è memorizzata in un programma per computer, può essere dichiarata come variabile di testo e gli unici valori accettati saranno quelli già nominati: Maschio , Femmina.
Tuttavia la stessa variabile sesso può essere dichiarato e memorizzato come numero intero se un file Maschio è assegnato 1 già Femmina il valore viene assegnato Due. È per questo motivo che le variabili categoriali vengono talvolta definite tipo enumerato.
La caratteristica principale delle variabili categoriali è che a differenza di altre variabili, come continue e discrete, non è possibile fare operazioni aritmetiche con esse. Tuttavia puoi fare statistiche con loro, come vedremo in seguito.
Indice articolo
- 1 Esempi
- 2 Classificazione delle variabili categoriali
- 2.1 Categorie nominali
- 2.2 Categorie ordinali
- 2.3 Categorie binarie
- 3 Statistiche con variabili categoriali
- 3.1 Rappresentazione grafica di variabili categoriali
- 4 Esercizi risolti
- 4.1 Esercizio 1
- 4.2 Esempio 2
- 4.3 Esempio 3
- 5 Riferimenti
Esempi
Notare i seguenti esempi di variabili categoriali e i loro possibili valori:
-Gruppo sanguigno, Intervallo di valori: A, B, AB, O
-Stato civile, Valori categoriali: Single (PER), Sposato (B), Vedovo (C) , Divorziato (D).
-Tipo di materiale, Categorie o valori: 1 = legno, 2 = metallo, 3 = plastica
-Modo di pagare, Valori o categorie: (1) Contanti, (2) Debito, (3) Trasferimento, (4) Credito
Negli esempi precedenti, un numero è stato associato a ciascuna categoria in modo del tutto arbitrario.
Si potrebbe quindi pensare che questa associazione numerica arbitraria la renda uguale ad a variabile quantitativa discreta, ma non lo è, poiché non è possibile eseguire operazioni aritmetiche con questi numeri.
Per illustrare l'idea, nella variabile Modo di pagare, l'operazione di somma non ha senso:
(1) Contanti + (2) Addebito non sarà mai uguale (3) Trasferimento
Classificazione delle variabili categoriali
La classifica si basa sul fatto che abbiano o meno una gerarchia implicita o se il numero di possibili risultati è superiore a due o due.
Una variabile categoriale con un solo risultato possibile non è una variabile, è una costante categoriale.
Categorie nominali
Quando non possono essere rappresentati da un numero o avere un ordine. Ad esempio la variabile: Tipo_materiale, tha valori nominali (Legno, metallo, plastica), non hanno gerarchia o ordine, anche quando un numero arbitrario è assegnato a ciascuna risposta o categoria.
Ordinale categoriale
Variabile: Rendimento scolastico
Valori nominali: Alto Medio basso
Sebbene i valori di questa variabile non siano numerici, hanno un ordine o una gerarchia implicita.
Categorie binarie
Si tratta di variabili nominali con due possibili risposte, ad esempio:
-Variabile: Risposta
-Valori nominali: Vero, Falso
Nota che la variabile Risposta non ha una gerarchia implicita e ha solo due possibili risultati, quindi è una variabile categoriale binaria.
Alcuni autori chiamano questo tipo variabile binaria, e non considerarlo appartenere al variabili categoriali che sono limitati a quelli con più di tre possibili categorie.
Statistiche con variabili categoriali
Le statistiche possono essere eseguite con variabili categoriali, nonostante non siano variabili numeriche o quantitative. Ad esempio, per conoscere la tendenza o il valore più probabile di una variabile categoriale, prendi Moda.
Moda è, in questo caso, il risultato o il valore più ripetuto di una variabile categoriale. Nelle variabili categoriali non è possibile calcolare né la media né la mediana.
La media non può essere calcolata perché non è possibile eseguire operazioni aritmetiche con variabili categoriali. Nemmeno la mediana, perché le variabili quantitative o categoriali non hanno un ordine o una gerarchia, quindi non è possibile determinare un valore centrale..
Rappresentazione grafica di variabili categoriali
Data una certa variabile categoriale, è possibile trovare la frequenza o il numero di volte con cui viene ripetuto un risultato di quella variabile. Se questo viene fatto per ogni risultato, è possibile creare un grafico della frequenza rispetto a ciascuna categoria o risultato..
Di seguito sono riportati alcuni esempi di come le variabili categoriali possono essere rappresentate graficamente.
Esercizi risolti
Esercizio 1
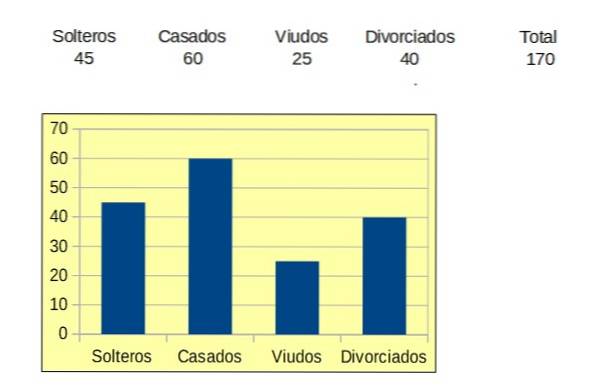
Una società ha registrazioni dei dati di 170 dipendenti. Una delle variabili che si trova in questi registri è: Stato civile. Questa variabile ha quattro categorie o valori possibili:
Single (PER), Sposato (B), Vedovo (C) , Divorziato (D).
Sebbene sia una variabile non numerica, è possibile sapere quanti dei record totali si trovano in una determinata categoria ed essere rappresentati sotto forma di un grafico a barre, come mostrato nella figura seguente:
Esempio 2
Un negozio di scarpe tiene traccia delle sue vendite. Tra le variabili che gestiscono i loro record c'è il colore della scarpa per ogni modello. La variabile:
Color_Shoe_Model_AW3
È categoriale e ha cinque possibili categorie o valori. Per ciascuna categoria di questa variabile viene sommato il numero di vendite e viene stabilita la loro percentuale. I risultati sono presentati nel grafico della figura seguente:
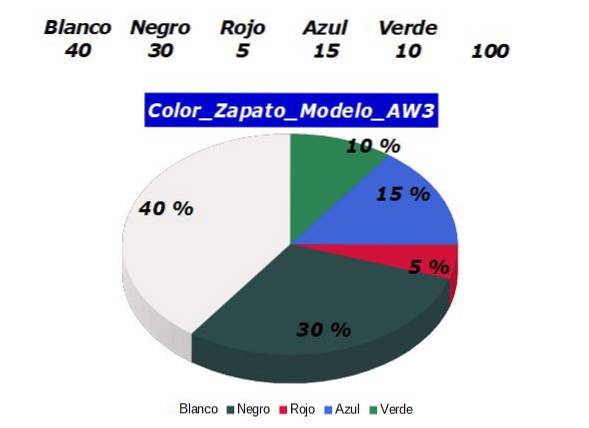
Si può quindi dire che il modello di scarpa AW3 in moda, quello che viene venduto più frequentemente è il bianca, seguito da vicino da Nero.
Si può anche dire che con una probabilità del 70% lo sarà la prossima scarpa venduta di questo modello bianca o Nero.
Queste informazioni possono essere utili per il negozio quando si effettuano nuovi ordini o potrebbero persino applicare sconti sui colori meno venduti a causa dell'eccesso di inventario..
Esempio 3
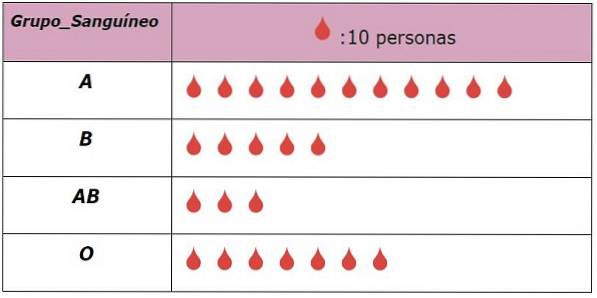
Per una determinata popolazione di donatori di sangue, si desidera rappresentare il numero di persone che appartengono a un determinato gruppo sanguigno. Un modo grafico per visualizzare i risultati è tramite un pittogramma, che è sullo sfondo una tabella.
La prima colonna rappresenta la variabile Gruppo sanguigno ei suoi possibili risultati o categorie. La seconda colonna ha la rappresentazione in forma iconica o pittorica del numero di persone in ciascuna categoria. Nel nostro esempio, una goccia rossa viene utilizzata come icona, ciascuna delle quali rappresenta 10 persone.
Riferimenti
- Khan Academy. Analisi dei dati categoriali. Estratto da: khanacademy.org
- Formule dell'universo. Variabile qualitativa. Estratto da: univesoformulas.com
- Minitab. Che sono variabili categoriali, discrete e continue. Recupero da: support.minitab.com
- Tutorial su Excel. Caratterizzazione delle variabili. Recupero da: help.xlslat.com.
- Wikipedia. Variabile statistica. Estratto da wikipedia.com
- Wikipedia. Variabile categoriale. Estratto da wikipedia.com
- Wikipedia. Variabile categoriale. Estratto da wikipedia.com



Nessun utente ha ancora commentato questo articolo.