
Triangoli storici, elementi, classificazione, proprietà

Il triangoli Sono figure geometriche piatte e chiuse, composte da tre lati. Un triangolo è determinato da tre linee che si intersecano a due a due, formando tre angoli tra loro. La forma triangolare, ricca di simbolismo, è presente in innumerevoli oggetti e come elemento di costruzione.
L'origine del triangolo si perde nella storia. Dalle prove archeologiche è noto che l'umanità primitiva lo conosceva bene, poiché i resti archeologici confermano che era usato in strumenti e armi.

È anche chiaro che gli antichi egizi avevano una solida conoscenza della geometria e in particolare della forma triangolare. Si riflettevano negli elementi architettonici dei suoi edifici monumentali.
Nel papiro Rhind ci sono formule per il calcolo delle aree di triangoli e trapezi, così come alcuni volumi e altri concetti di trigonometria rudimentale.
Da parte loro, è noto che i babilonesi erano in grado di calcolare l'area del triangolo e di altre figure geometriche, che usavano per scopi pratici, come le divisioni delle terre. Erano anche ben informati su molte proprietà dei triangoli.
Tuttavia, furono gli antichi greci a sistematizzare molti dei concetti geometrici prevalenti oggi, sebbene gran parte di questa conoscenza non fosse esclusiva, poiché era sicuramente condivisa con queste altre antiche civiltà..
Indice articolo
- 1 Elementi del triangolo
- 1.1 Notazione
- 2 tipi di triangoli
- 2.1 Congruenza dei triangoli
- 2.2 Somiglianza dei triangoli
- 3 Proprietà
- 4 teoremi
- 4.1 Primo teorema di Talete
- 4.2 Secondo teorema di Talete
- 4.3 Il teorema di Pitagora
- 5 L'area di un triangolo
- 6 Esempi di triangoli
- 6.1 Esempio 1
- 6.2 Esempio 2
- 6.3 Esempio 3
- 7 Esercizi
- 7.1 Esercizio 1
- 7.2 Esercizio 2
- 8 Riferimenti
Elementi triangolari
Gli elementi di qualsiasi triangolo sono indicati nella figura seguente. Ce ne sono tre: vertici, lati e angoli.
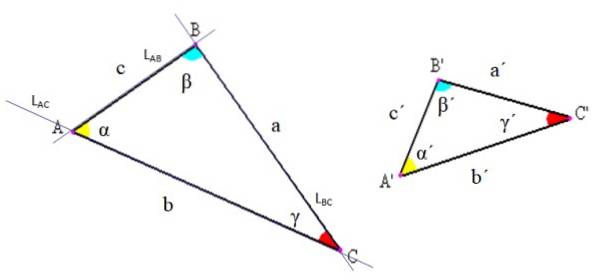
-Vertici: sono i punti di intersezione delle rette i cui segmenti determinano il triangolo. Nella figura sopra, ad esempio, la linea LAC contenente il segmento AC, interseca la linea LAB contenente il segmento AB proprio nel punto A.
-Lati: tra ogni coppia di vertici viene disegnato un segmento di linea che costituisce un lato del triangolo. Questo segmento può essere indicato con le lettere finali o utilizzando una lettera specifica per chiamarlo. Nell'esempio in figura 2, il lato AB è anche chiamato "c".
-Angoli: Tra ogni lato con un vertice comune ha origine un angolo, il cui vertice coincide con quello del triangolo. Generalmente l'angolo è indicato con una lettera greca, come si diceva all'inizio.
Per costruire un particolare triangolo, con una data forma e dimensione, basta avere uno dei seguenti set di dati:
-Tutti e tre i lati, abbastanza ovvio per un triangolo.
-Due lati e l'angolo tra di loro e immediatamente viene disegnato il lato rimanente.
-Due angoli (interni) e il lato tra di loro. Per estensione vengono disegnati i due lati mancanti e il triangolo è pronto.
Notazione
Generalmente, nella notazione triangolare vengono utilizzate le seguenti convenzioni: i vertici sono indicati con lettere latine maiuscole, i lati con lettere latine minuscole e gli angoli con lettere greche (vedi figura 2).
In questo modo il triangolo viene chiamato in base ai suoi vertici. Ad esempio, il triangolo a sinistra nella figura 2 è il triangolo ABC e quello a destra è il triangolo A'B'C '.
È anche possibile utilizzare altre notazioni; per esempio, l'angolo α nella Figura 2 è indicato come BAC. Nota che la lettera del vertice va nel mezzo e le lettere sono scritte in senso antiorario.
Altre volte viene inserito un accento circonflesso per indicare l'angolo:
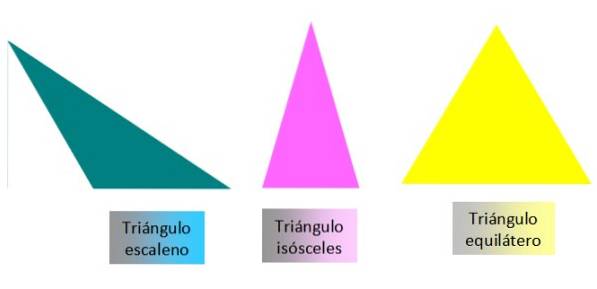
α = ∠A
Tipi di triangoli
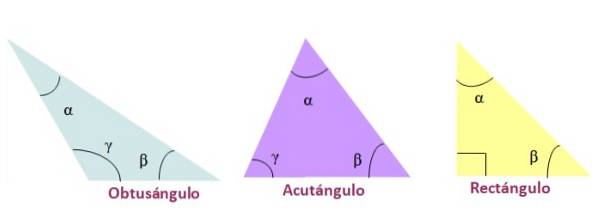
Esistono diversi criteri per classificare i triangoli. La cosa più comune è classificarli in base alla misura dei loro lati o in base alla misura dei loro angoli. A seconda della misura dei loro lati, i triangoli possono essere: scaleni, isosceli o equilateri:
-Scaleno: i suoi tre lati sono diversi.
-Isoscele: ha due lati uguali e un lato diverso.
-Equilatero: tutti e tre i lati sono uguali.

Secondo la misura dei loro angoli, i triangoli hanno questo nome:
-Angolo ottuso, se uno degli angoli interni è maggiore di 90º.
-Angolo acuto, quando i tre angoli interni del triangolo sono acuti, cioè inferiori a 90º
-Rettangolo, nel caso in cui uno dei suoi angoli interni sia di 90º. I lati che formano 90 ° sono chiamati gambe e il lato opposto all'angolo retto è l'ipotenusa..
Congruenza dei triangoli
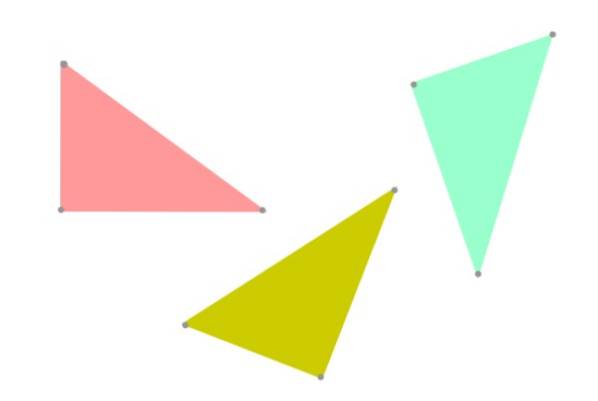
Quando due triangoli hanno la stessa forma e le stesse dimensioni, si dice che siano congruenti. Ovviamente la congruenza è correlata all'uguaglianza, quindi perché in geometria si parla di "due triangoli congruenti" invece di "due triangoli uguali"?
Ebbene, si preferisce usare il termine "congruenza" per attenersi alla verità, poiché due triangoli possono avere la stessa forma e dimensione, ma essere orientati in modo diverso nel piano (vedi figura 3). Dal punto di vista della geometria, non sarebbero più rigorosamente gli stessi.
Criteri di congruenza
Due triangoli sono congruenti se si verifica una delle seguenti condizioni:
-Tutti e tre i lati misurano lo stesso (di nuovo questo è il più ovvio).
-Hanno due lati identici e con lo stesso angolo tra di loro.
-Entrambi hanno due angoli interni identici e il lato tra questi angoli misura lo stesso.
Come si può vedere, si tratta di due triangoli che soddisfano le condizioni necessarie in modo che quando vengono costruiti, la loro forma e dimensione siano esattamente le stesse..
I criteri di congruenza sono molto utili, poiché in pratica innumerevoli pezzi e parti meccaniche devono essere fabbricati in serie, in modo tale che le loro misure e forma siano esattamente le stesse.
Somiglianza dei triangoli
Un triangolo è simile a un altro se hanno la stessa forma, anche se di dimensioni diverse. Per assicurarsi che la forma sia la stessa, è necessario che gli angoli interni abbiano lo stesso valore e che i lati siano proporzionali..
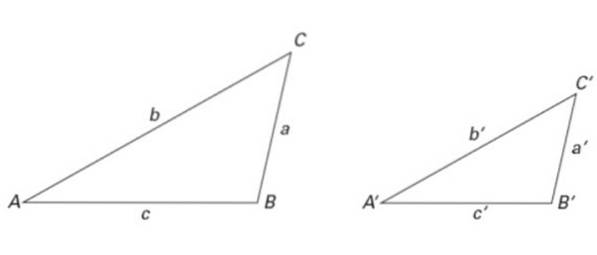
Anche i triangoli nella figura 2 sono simili, come quelli nella figura 6. In questo modo:
∠ LA = ∠ A ', ∠ B = ∠ B 'e ∠ C = ∠ C '
Per quanto riguarda i lati, valgono i seguenti rapporti di somiglianza:
a / a '= b / b' = c / c '
Proprietà
Le proprietà fondamentali dei triangoli sono le seguenti:
-La somma degli angoli interni di qualsiasi triangolo è sempre 180º.
-Per ogni triangolo, la somma dei suoi angoli esterni è uguale a 360 °.
- Un angolo esterno di un triangolo è uguale alla somma dei due angoli interni non adiacenti a detto angolo.
Teoremi
Primo teorema di Talete
Sono attribuiti al filosofo e matematico greco Talete di Mileto, che ha sviluppato diversi teoremi relativi alla geometria. Il primo di essi stabilisce quanto segue:
Se più linee parallele intersecano due linee trasversali, in esse vengono determinati segmenti proporzionali.
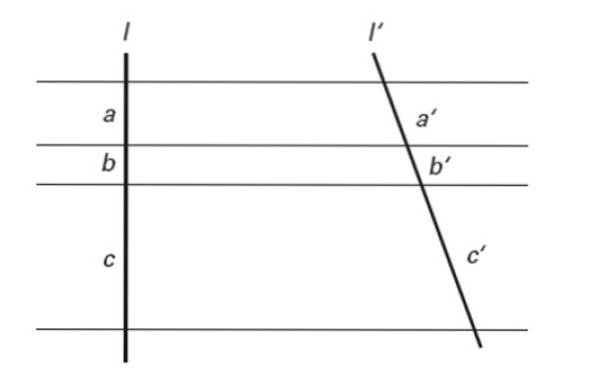
In altre parole:
a / a '= b / b' = c / c '
Il primo teorema di Talete è applicabile a un triangolo, ad esempio abbiamo il triangolo blu ABC a sinistra, che è tagliato dai paralleli rossi a destra:
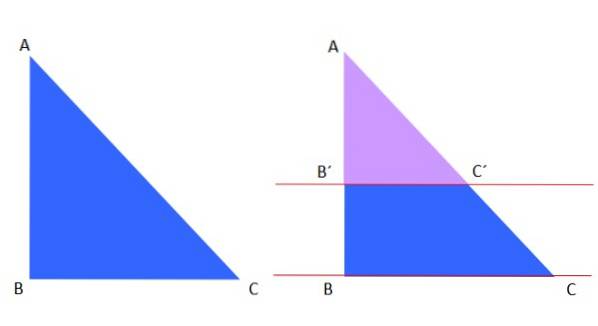
Il triangolo viola AB'C 'è simile al triangolo blu ABC, quindi, secondo il teorema di Talete, si può scrivere quanto segue:
AB '/ AC' = AB / AC
Ed è coerente con quanto spiegato in precedenza nel segmento della somiglianza dei triangoli. A proposito, le linee parallele possono anche essere verticali o parallele all'ipotenusa e triangoli simili si ottengono allo stesso modo.
Secondo teorema di Talete
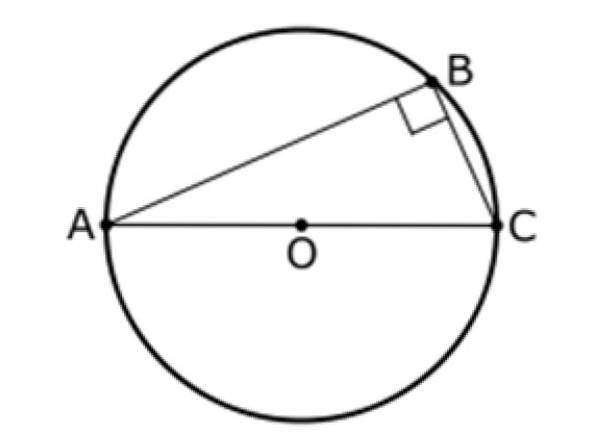
Questo teorema si riferisce anche a un triangolo e un cerchio con centro O, come quelli mostrati sotto. In questa figura, AC è un diametro della circonferenza e B è un punto su di essa, essendo B diverso da A e B.
Il secondo teorema di Talete afferma che:
L'angolo tra i segmenti AB e BC è sempre di 90º, quindi il triangolo ABC è retto.
Il teorema di Pitagora
Questo è uno dei teoremi più famosi della storia. È dovuto al matematico greco Pitagora di Samo (569 - 475 a.C.) ed è applicabile a un triangolo rettangolo. Dice così:
La somma dei quadrati delle lunghezze delle gambe del triangolo rettangolo è uguale alla lunghezza dell'ipotenusa al quadrato.
Se prendiamo come esempio il triangolo blu nella figura 8, o il triangolo viola, poiché entrambi sono rettangoli, si può affermare che:
ACDue = ABDue + AVANTI CRISTODue (triangolo blu)
AC 'Due = AB 'Due + AVANTI CRISTO 'Due (triangolo viola)
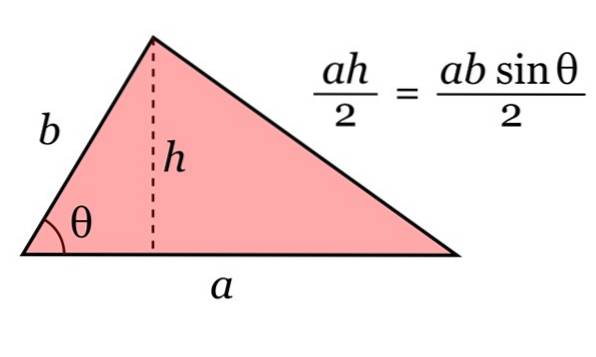
L'area di un triangolo
L'area del triangolo è data dal prodotto della sua base per e la tua altezza h, diviso per 2. E per trigonometria, questa altezza può essere scritta come h = b sinθ.
Esempi di triangoli
Esempio 1
Si dice che attraverso il suo primo teorema, Talete riuscì a misurare l'altezza della Grande Piramide d'Egitto, una delle 7 meraviglie del mondo antico, misurando l'ombra che proiettava al suolo e quella proiettata da un paletto conficcato nel terreno..
Questo è lo schema della procedura seguita da Tales:
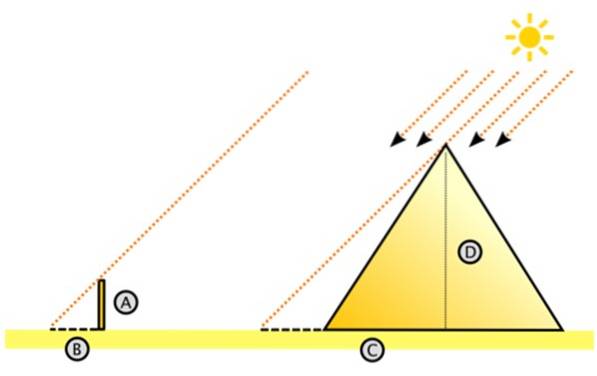
Talete presumeva correttamente che i raggi del sole colpissero parallelamente. Con questo in mente, ha immaginato il grande triangolo rettangolo sulla destra.
D è l'altezza della piramide e C è la distanza dal suolo misurata dal centro all'ombra proiettata dalla piramide sul pavimento del deserto. Può essere laborioso misurare C, ma è certamente più facile che misurare l'altezza della piramide.
A sinistra c'è il piccolo triangolo, con le gambe A e B, dove A è l'altezza del paletto conficcato verticalmente nel terreno e B è l'ombra che proietta. Entrambe le lunghezze sono misurabili, così come C (C è uguale alla lunghezza dell'ombra + metà della lunghezza della piramide).
Quindi, per somiglianza dei triangoli:
A / B = D / C
E l'altezza della Grande Piramide risulta essere: D = C. (A / B)
Esempio 2
Le capriate nell'edilizia civile sono strutture costituite da sottili barre diritte incrociate di legno o metallo, che vengono utilizzate come supporto in molti edifici. Sono anche conosciuti come reticoli, tralicci o reticoli (capriata in inglese).
In essi i triangoli sono sempre presenti, poiché le barre sono interconnesse in punti chiamati nodi, che possono essere fissi o articolati..

Esempio 3
Il metodo noto come triangolazione consente di ottenere la posizione di punti inaccessibili conoscendo altre distanze che sono più facili da misurare, a condizione che si formi un triangolo che includa la posizione desiderata tra i suoi vertici..
Ad esempio, nella figura seguente vogliamo sapere dove si trova la nave in mare, indicata come B.
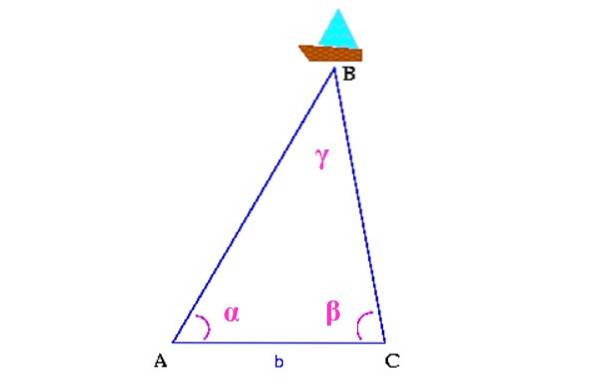
Per prima cosa si misura la distanza tra due punti della costa, che in figura sono A e C.Successivamente si determinano gli angoli α e β, con l'ausilio di a teodolite, un dispositivo utilizzato per misurare gli angoli verticali e orizzontali.
Con tutte queste informazioni, viene costruito un triangolo nel cui vertice superiore è la nave. Rimarrebbe da calcolare l'angolo γ, usando le proprietà dei triangoli e le distanze AB e CB usando la trigonometria, per determinare la posizione della nave in mare.
Formazione
Esercizio 1
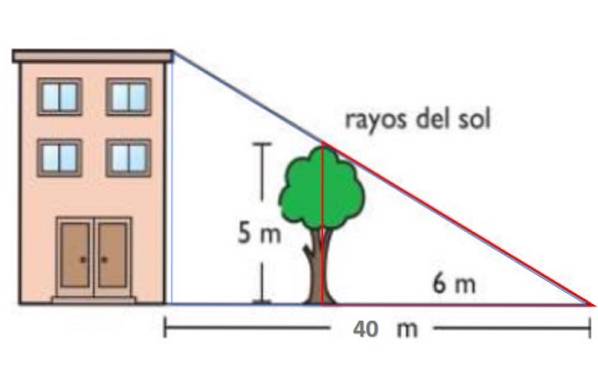
Nella figura mostrata, i raggi del sole sono paralleli. In questo modo l'albero alto 5 metri proietta un'ombra sul terreno di 6 metri. Allo stesso tempo, l'ombra dell'edificio è di 40 metri. Seguendo il primo teorema di Talete, trova l'altezza dell'edificio.
Soluzione
Il triangolo rosso ha i lati rispettivamente di 5 e 6 metri, mentre quello blu ha altezza H - l'altezza dell'edificio - e base 40 metri. Entrambi i triangoli sono simili, quindi:
H / 40 = 5/6 → H = 40. (5/6) m = 33,3 m
Esercizio 2
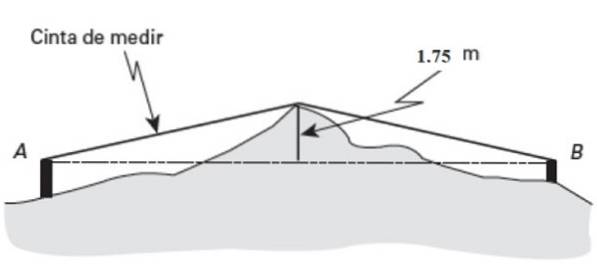
Devi conoscere la distanza orizzontale tra due punti PER Y B, ma si trovano su un terreno molto irregolare.
Circa il punto medio (Pm) di questo terreno spicca una prominenza di 1,75 metri di altezza. Se il metro a nastro indica 26 metri di lunghezza misurati da A alla prominenza e 27 metri da B allo stesso punto, trova la distanza AB.
Soluzione
Il teorema di Pitagora è applicato a uno dei due triangoli rettangoli nella figura. A partire da quello a sinistra:
Ipotenusa = c = 26 metri
Altezza = a = 1,75 metri
APm = (26Due - 1.75Due)1/2 = 25,94 m
Ora applica Pitagora nel triangolo a destra, questa volta c = 27 metri, a = 1,75 metri. Con questi valori:
BPm= (27Due - 1.75Due)1/2 = 26,94 m
La distanza AB si trova sommando questi risultati:
AB = 25,94 m + 26,94 m = 52,88 m.
Riferimenti
- Baldor, J. A. 1973. Plane and Space Geometry. Centro culturale americano.
- Barredo, D. La geometria del triangolo. Recupero da: ficus.pntic.mec.es.
- Jiménez, R. 2010. Matematica II. Geometria e trigonometria. Seconda edizione. Pearson.
- Wentworth, G. Plane Geometry. Estratto da: gutenberg.org.
- Wikipedia. Triangolo. Estratto da: es. wikipedia.org.


Nessun utente ha ancora commentato questo articolo.