Formule di tiro verticale, equazioni, esempi

Il tiro verticale È un movimento che avviene sotto l'azione di un campo di forza, comunemente quello della gravità, e può essere ascendente o discendente. È anche conosciuto con il nome di lancio verticale.

L'esempio più immediato è lanciare verso l'alto (o verso il basso se preferisci) una palla con la mano, ovviamente, assicurandoti di farlo in direzione verticale. Indipendentemente dalla resistenza dell'aria, il movimento che la palla segue si adatta perfettamente al modello MRUV (Uniformly Varied Rectilinear Motion)..

Il tiro verticale è un movimento ampiamente studiato nei corsi introduttivi di fisica, in quanto è un campione del movimento in una dimensione, un modello molto semplice e utile.

Questo modello non solo può essere utilizzato per studiare la cinematica degli oggetti sotto l'azione della gravità, ma anche, come si vedrà più avanti, descrive il movimento delle particelle nel mezzo di un campo elettrico uniforme..

Indice articolo

• 1 Formule ed equazioni
  • 1.1 Equazioni del tiro verticale
• 2 esempi
  • 2.1 Esempio di lavoro 1
  • 2.2 Esempio lavorato 2
• 3 Riferimenti

Formule ed equazioni

La prima cosa che serve è un sistema di coordinate che indichi l'origine e la etichetti con una lettera, che nel caso dei movimenti verticali è la lettera "Y".

Quindi viene selezionata la direzione positiva +Y, che di solito è verso l'alto e il senso -Y che di solito viene rimosso (vedere la figura 2). Tutto questo a meno che il risolutore del problema non decida diversamente, poiché un'altra opzione è quella di prendere la direzione del movimento come positiva, qualunque essa sia..

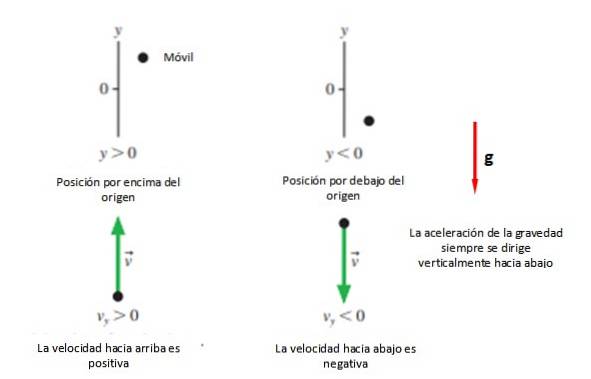
In ogni caso, si raccomanda che l'origine coincida con il punto di lancio. Y_o, perché in questo modo le equazioni sono semplificate, anche se puoi prendere qualsiasi posizione desideri per iniziare a studiare il moto.

Equazioni del tiro verticale

Una volta stabilito il sistema di coordinate e l'origine, passiamo alle equazioni. Le grandezze che descrivono il movimento sono:

-Velocità iniziale v_o

-Accelerazione per

-Velocità v

-Posizione iniziale X_o

-Posizione X

-Dislocamento DX

-Tempo metereologico t

Tutti tranne il tempo sono vettori, ma poiché è un movimento unidimensionale con una certa direzione, ciò che conta è usare i segni + o - per indicare dove sta andando la grandezza in questione. In caso di pescaggio verticale, la gravità va sempre verso il basso e, se non diversamente specificato, viene assegnato un segno -.

Di seguito sono riportate le equazioni adattate per lo sformo verticale, sostituendo "X"per"Y"Y"per"per"g". Inoltre, verrà incluso subito il segno (-) corrispondente alla gravità diretta verso il basso:

1) Posizione: y = y_o + v_o.t - ½ g.t^Due

2) Velocità: v = v_o - g.t

3) Velocità in funzione dello spostamento ΔY: v^Due = v_o^Due - 2 g. ΔY

Esempi

Di seguito sono riportati esempi di applicazioni per riprese verticali. Nella sua risoluzione, si deve tener conto di quanto segue:

-"g”Ha un valore costante che mediamente è di 9,8 m / s^Due o circa 10 m / s^Due se si preferisce per facilitare i calcoli quando non è richiesta troppa precisione.

-quando v_o va bene 0, queste equazioni si riducono a quelle di caduta libera.

-Se il lancio è verso l'alto, l'oggetto deve avere una velocità iniziale che gli consenta di muoversi. Una volta in movimento, l'oggetto raggiunge un'altezza massima che dipenderà da quanto è grande la velocità iniziale. Ovviamente, maggiore è l'altitudine, maggiore sarà il tempo che il cellulare trascorrerà in aria.

-L'oggetto ritorna al punto di partenza con la stessa velocità con cui è stato lanciato, ma la velocità è diretta verso il basso.

-Per un lancio verticale verso il basso, maggiore è la velocità iniziale, prima l'oggetto colpirà il suolo. Qui la distanza percorsa è impostata in base all'altezza selezionata per il lancio.

-Nel lancio verticale verso l'alto, il tempo impiegato dal mobile per raggiungere l'altezza massima viene calcolato facendo v = 0 nell'equazione 2) della sezione precedente. Questo è il tempo massimo t_max:

0 = v_o - g. t_max ⇒ t_max = v_o / g

-Il altezza massima Y_max viene cancellato dall'equazione 3) della sezione precedente facendo lo stesso v = 0:

0 = v_o^Due - 2 g. Δy ⇒ 0 = v_o^Due - 2 g. (Y_max - Y_o) ⇒ e_max = e_o  + v_o^Due / 2 g

sì Y_o = 0, Si riduce a:

Y_max = v_o^Due / 2 g

Esempio lavorato 1

Si lancia una palla verticalmente verso l'alto con v_o = 14 m / s, dalla sommità di un edificio alto 18 m. La palla può continuare a scendere sul marciapiede. Calcolare:

a) L'altezza massima raggiunta dalla palla rispetto al suolo.

b) Il tempo che era nell'aria (tempo di volo).

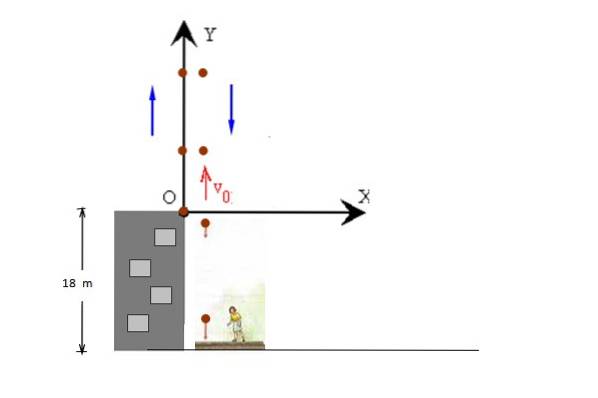
Soluzione

La figura mostra i movimenti di sollevamento e abbassamento della palla separatamente per chiarezza, ma entrambi si verificano lungo la stessa linea. La posizione iniziale è presa a y = 0, in modo che la posizione finale sia y = - 18 m.

a) L'altezza massima misurata dal tetto dell'edificio è Y_max = v_o^Due / 2 g e dall'affermazione possiamo leggere che la velocità iniziale è +14 m / s, quindi:

Y_max = (14 m / s)^Due / 2 x 9,8 m / s^Due = 10 m (Riguardo al tetto)

H_max = 10 m + 18 m = 28 m (Riguardo al marciapiede).

b) Per trovare il file tempo totale o tempo di volo la palla dura in aria, verrà utilizzata l'equazione y = y_o + v_o.t - ½ g.t^Due, con i seguenti valori e segni:

y = - 18 m

Y_o = 0 m

v_o = +14 m / s

Sostituzione:

- 18 = 14.t - ½ 9,8 .t^Due

- 4,9 t^Due+14.t + 18 = 0 

4,9 t^Due-14.t - 18 = 0

È un'equazione di secondo grado facilmente risolvibile con l'aiuto di una calcolatrice scientifica o utilizzando il risolutore. Le soluzioni sono: 3,82 e -0,96. La soluzione negativa viene scartata poiché, trattandosi di un tempo, manca di senso fisico.

Il tempo di volo della palla è di 3,82 secondi.

Esempio lavorato 2

Una particella caricata positivamente con q = +1,2 millicoulomb (mC) e massa m = 2,3 x 10 ^-10 Kg è proiettato verticalmente verso l'alto, partendo dalla posizione mostrata in figura e con velocità iniziale v_o = 30 km / s.

Tra le piastre cariche c'è un campo elettrico E uniforme, diretto verticalmente verso il basso e con magnitudo 780 N / C. Se la distanza tra le piastre è di 18 cm, la particella entrerà in collisione con la piastra superiore? Trascura l'attrazione gravitazionale sulla particella, poiché è estremamente leggera.

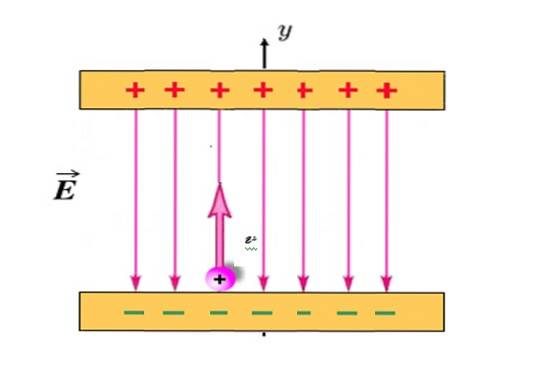
Soluzione

In questo problema il campo elettrico E è quello che produce una forza F e la conseguente accelerazione. Essendo caricata positivamente, la particella è sempre attratta dalla piastra inferiore, tuttavia quando viene proiettata verticalmente verso l'alto raggiungerà un'altezza massima per poi tornare alla piastra inferiore, proprio come la palla negli esempi precedenti..

Per definizione di campo elettrico:

E = F / q = m.a / q ⇒ a = q.E / m

È necessario utilizzare questa equivalenza prima di sostituire i valori:

1 mC = 1 x 10^-3 C

Quindi l'accelerazione è:

a = 1,2 x 10^-3 x 780 / 2,3 x 10 ^-10SM^Due = 4,07 x 10⁹ SM^Due

Per l'altezza massima, viene utilizzata la formula della sezione precedente, ma invece di utilizzare "g"Questo valore di accelerazione viene utilizzato:

Y_max = v_o^Due / 2a = (30.000 m / s)^Due/ 2 x 4,07 x 10⁹ SM^Due = 0,11 m = 11 cm

Non entra in collisione con la piastra superiore, poiché si trova a 18 cm dal punto di partenza e la particella raggiunge solo 11 cm.

Riferimenti

1. Kirkpatrick, L. 2007. Fisica: uno sguardo al mondo. 6^ta Edizione abbreviata. Cengage Learning. 23 - 27.
2. Rex, A. 2011. Fondamenti di fisica. Pearson. 33 - 36
3. Sears, Zemansky. 2016. Fisica universitaria con fisica moderna. 14^th. Ed. Volume 1. 50 - 53.
4. Serway, R., Vulle, C. 2011. Fondamenti di fisica. 9^{n / A} Ed. Cengage Learning. 43 - 55.
5. Wilson, J. 2011. Fisica 10. Pearson Education. 133 - 149.