
Spiegazione della seconda condizione di equilibrio, esempi, esercizi
Il seconda condizione di equilibrio stabilisce che la somma delle coppie o momenti prodotti da tutte le forze agenti su un corpo, indipendentemente dal punto in cui vengono calcolate, deve essere annullata in modo che detto corpo sia in equilibrio statico o dinamico.
Indica la coppia o il momento di forza con la lettera greca τ, matematicamente si esprime così:
∑ τ = 0

La lettera in grassetto indica la natura vettoriale del momento, che deve essere annullata rispetto a qualsiasi punto scelto come centro di rotazione. In questo modo, l'annullamento della coppia netta garantisce che l'oggetto non inizi a ruotare o ribaltarsi..
Tuttavia, se l'oggetto stava già ruotando in precedenza e la coppia netta scompare improvvisamente, la rotazione continuerà, ma con velocità angolare costante.
La seconda condizione di equilibrio è usata insieme alla prima condizione, che dice che la somma delle forze su un corpo deve essere zero, in modo che non si traduca, o che se lo fa, è con moto rettilineo uniforme:
∑ F = 0
Entrambe le condizioni si applicano ai corpi estesi, quelli le cui dimensioni sono misurabili. Quando si assume che un oggetto sia una particella, non ha senso parlare di rotazioni e la prima condizione è sufficiente a garantire l'equilibrio.
Esempi
La seconda condizione di equilibrio si rivela in innumerevoli situazioni:
Mentre sali la scala
Quando si sostiene una scala sul pavimento e sul muro, è necessario un attrito sufficiente, soprattutto sul pavimento, per garantire che la scala non scivoli. Se proviamo a salire su una scala appoggiata su un pavimento oleoso, bagnato o scivoloso, non è difficile prevedere che cadremo.
Per poter utilizzare la scala con sicurezza, è necessario che sia in equilibrio statico durante la salita e quando si trova sul gradino richiesto.
Spostare un armadio
Quando si vuole spostare un mobile alto come un armadio, o qualsiasi pezzo la cui altezza sia maggiore della sua larghezza, è conveniente spingere su un punto basso, per evitare il ribaltamento, in questo modo è più probabile che il i mobili scivoleranno invece di girare e si sdraieranno.
In tali circostanze il mobile non è necessariamente in equilibrio, in quanto potrebbe muoversi velocemente, ma almeno non si ribalterebbe.
Balconi
I balconi che sporgono dagli edifici dovrebbero essere costruiti facendo in modo che anche se ci sono molte persone in cima, non si ribalti e crolli.
Dielettrici nei campi elettrici esterni
Posizionando un materiale dielettrico in un campo elettrico esterno, le molecole si muovono e ruotano fino ad assumere una posizione di equilibrio, creando un campo elettrico all'interno del materiale..
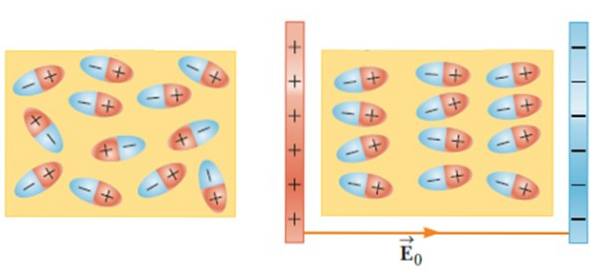
Questo effetto aumenta la capacità di un condensatore quando un materiale come vetro, gomma, carta o olio viene inserito tra i suoi telai..
Segni e lampade
È comune per molti locali appendere avvisi sul muro dell'edificio, in modo che siano visibili ai passanti.
Il poster è trattenuto da una barra e da un cavo, entrambi fissati al muro tramite staffe. Le varie forze che agiscono devono garantire che il poster non cada, per cui entrano in gioco le due condizioni di equilibrio.
Un riflettore può essere posizionato in questo modo anche in un parco, come nella figura seguente:
Come calcolare la coppia netta o il momento netto di una forza?
La coppia o il momento di una forza, indicato da τ o M in alcuni testi è sempre calcolato rispetto ad un punto in cui passa l'asse di rotazione.
È definito come il prodotto vettoriale tra il vettore di posizione r, cioè diretto da detto asse al punto di applicazione della forza e della forza F:
τ = r × F
Essendo un vettore, è necessario esprimere la coppia dando la sua grandezza, direzione e senso. La grandezza è data da:
τ = rF.sen θ
Regola della mano destra per prodotto vettoriale
Quando il problema è nel piano, la direzione della coppia è perpendicolare alla carta o allo schermo e la direzione è determinata dalla regola della mano destra, in cui il dito indice punta verso r, dito medio verso F e il pollice punta verso l'interno o l'esterno della carta.
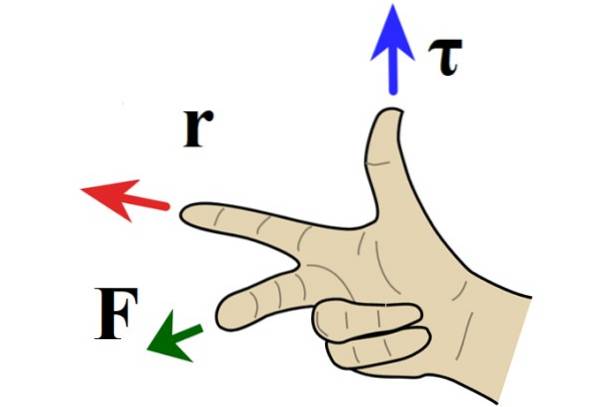
Quando la coppia punta fuori dalla carta, la rotazione è in senso antiorario e per convenzione viene assegnato un segno positivo. Se invece la coppia è diretta verso l'interno della lama, la rotazione è oraria e negativa..
Per trovare la coppia netta, viene scelto un punto conveniente per il calcolo, che può essere quello in cui agisce la maggior quantità di forze. In questo caso il momento di queste forze è zero, poiché ha un vettore di posizione r di magnitudine 0.
Puoi scegliere qualsiasi punto che offra informazioni sufficienti per risolvere l'ignoto che richiede la risoluzione del problema. Vediamolo più in dettaglio di seguito.
Esercizio risolto
Il riflettore nella figura seguente ha una massa di 20 kg ed è sostenuto da una sottile barra orizzontale, di massa e lunghezza L trascurabili, incernierata ad un palo. Il cavo, anche leggero, che aiuta a sostenere il riflettore forma un angolo θ = 30º con la barra. Calcolare:
a) La tensione nel cavo
b) L'entità della forza F che il palo esercita sulla barra attraverso la cerniera.
Soluzione
Applicheremo la prima condizione di equilibrio ∑ F = 0 alle forze mostrate nel diagramma:
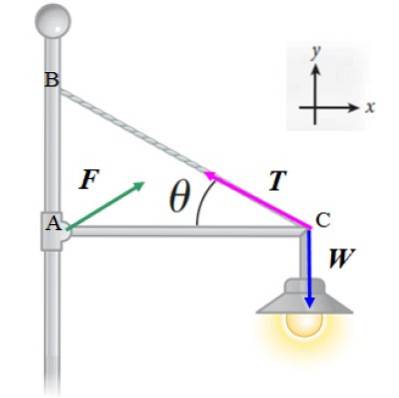
F + T + W = 0
Notare che l'ampiezza e la direzione di F devono ancora essere determinati, ma assumiamo che abbia due componenti: FX e FY. In questo modo otteniamo due equazioni:
FX -T. cos θ = 0
FY - W + T⋅ sin θ = 0
Ora applichiamo la seconda condizione di equilibrio, scegliendo il punto A, poiché non conosciamo l'ampiezza di F né quello di T. Scegliendo questo punto, il vettore rPER è nullo, quindi il momento di F è nullo e la grandezza di F non apparirà nell'equazione:
-W⋅L + T⋅sen θ⋅L = 0
Perciò:
T.sen θ.L = W.L
T = W / sin θ = (20 kg x 9,8 m / sDue) / Peccato 30º = 392 N
Conoscendo l'ampiezza di T possiamo risolvere per la componente FX:
FX = T⋅ cos θ = 392 cos 30º N = 339. 5 N
E poi il componente FY:
FY = W - T⋅ sin θ = (20 kg x 9,8 m / sDue) - 392⋅sin 30º = 0
Quindi possiamo esprimere F Così:
F = 339,5 N X
È quindi una forza orizzontale. Questo perché abbiamo considerato che la barra avesse un peso trascurabile.
Se il punto C fosse stato scelto per calcolare il momento risultante, i vettori rT Y rW sono nulli, quindi:
M = FeL = 0
Si conclude che FY = 0. In questo modo:
- W + T⋅ sin θ = 0
T = W / sin θ
Che è lo stesso risultato ottenuto inizialmente scegliendo il punto A come luogo in cui passa l'asse di rotazione.
Temi di interesse
Condizioni di equilibrio.
Prima condizione di equilibrio.
Riferimenti
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
- Figueroa, D. (2005). Serie: Fisica per la scienza e l'ingegneria. Volume 4. Sistemi di particelle. A cura di Douglas Figueroa (USB).
- Giancoli, D. 2006. Fisica: principi con applicazioni. 6 °. Ed prentice hall.
- Sears, Zemansky. 2016. Fisica universitaria con fisica moderna. 14th. Ed. Volume 1.
- Serway, R., Jewett, J. (2008). Fisica per la scienza e l'ingegneria. Volume 1. 7th. Ed. Cengage Learning.


Nessun utente ha ancora commentato questo articolo.