
Cos'è un geoide?
Il geoide La figura della Terra è la superficie teorica del nostro pianeta, determinata dal livello medio degli oceani e con una forma abbastanza irregolare. Matematicamente è definita come la superficie equipotenziale del potenziale gravitazionale effettivo della Terra, a livello del mare.
Essendo una superficie immaginaria (non materiale), attraversa continenti e montagne, come se tutti gli oceani fossero collegati da canali d'acqua che attraversano masse di terra..

La Terra non è una sfera perfetta, poiché la rotazione attorno al suo asse la trasforma in una sorta di palla appiattita dai poli, con valli e montagne. Ecco perché la forma dello sferoide è ancora imprecisa.
Questa stessa rotazione aggiunge una forza centrifuga alla forza di gravità terrestre, la cui forza risultante o effettiva non punta al centro della Terra, ma ha un certo potenziale gravitazionale ad essa associato..
A ciò si aggiungono gli incidenti geografici che creano irregolarità di densità, e quindi la forza di attrazione gravitazionale in alcune zone cessa definitivamente di essere centrale..
Così gli scienziati, a cominciare da C. F. Gauss, che ha ideato il geoide originale nel 1828, hanno creato un modello geometrico e matematico per rappresentare la superficie terrestre in modo più accurato..
Per questo si assume un oceano fermo, senza maree né correnti oceaniche e con densità costante, la cui altezza serve da riferimento. La superficie terrestre viene quindi considerata leggermente ondulata, aumentando dove la gravità locale è maggiore e affondando quando diminuisce.
In queste condizioni l'accelerazione di gravità effettiva sia sempre perpendicolare alla superficie i cui punti sono allo stesso potenziale e il risultato è il geoide, che è irregolare poiché l'equipotenziale non è simmetrico.
Indice articolo
- 1 Fondazione fisica del geoide
- 1.1 Il potenziale gravitazionale della Terra
- 2 Differenze tra geoide ed ellissoide
- 2.1 Le ondulazioni del geoide
- 3 Vantaggi di rappresentare la Terra come un geoide
- 4 Riferimenti
Fondamento fisico del geoide
Per determinare la forma del geoide, che è stata affinata nel tempo, gli scienziati hanno effettuato molte misurazioni, tenendo conto di due fattori:
- Il primo è che il valore di g, campo gravitazionale terrestre equivalente all'accelerazione di gravità, dipende dalla latitudine: massima ai poli e minima all'equatore.
- La seconda è che, come abbiamo detto prima, la densità della Terra non è omogenea. Ci sono luoghi in cui aumenta perché le rocce sono più dense, c'è un accumulo di magma o c'è molto terreno in superficie, come ad esempio una montagna.
Dove la densità è maggiore, g così è. Notare che g è un vettore ed è per questo che è indicato in grassetto.
Il potenziale gravitazionale della Terra
Per definire il geoide è necessario il potenziale dovuto alla gravità, per cui il campo gravitazionale deve essere definito come la forza gravitazionale per unità di massa.
Se una massa di prova m è posto in detto campo, la forza esercitata dalla Terra su di esso è il suo peso P = mg, quindi l'ampiezza del campo è:
Forza / massa = P / m = g
Conosciamo già il suo valore medio: 9,8 m / sDue e se la Terra fosse sferica, sarebbe diretta verso il suo centro. Allo stesso modo, secondo la legge di gravitazione universale di Newton:
P = Gm M / rDue
Dove M è la massa della Terra e G è la costante universale di gravitazione. Quindi l'ampiezza del campo gravitazionale g è:
g = GM / rDue
Assomiglia molto a un campo elettrostatico, quindi è possibile definire un potenziale gravitazionale analogo a quello elettrostatico:
V = -GM / r
La costante G è la costante universale di gravitazione. Ebbene, si chiamano le superfici su cui il potenziale gravitazionale ha sempre lo stesso valore superfici equipotenziali Y g è sempre perpendicolare a loro, come detto prima.
Per questa particolare classe di potenziale, le superfici equipotenziali sono sfere concentriche. Il lavoro richiesto per spostare una massa su di essi è zero, perché la forza è sempre perpendicolare a qualsiasi percorso sull'equipotenziale.
Componente laterale dell'accelerazione di gravità
Poiché la Terra non è sferica, l'accelerazione di gravità deve avere una componente laterale gl a causa dell'accelerazione centrifuga, causata dal movimento rotatorio del pianeta attorno al suo asse.
La figura seguente mostra questo componente in verde, la cui grandezza è:
gl = ωDueper
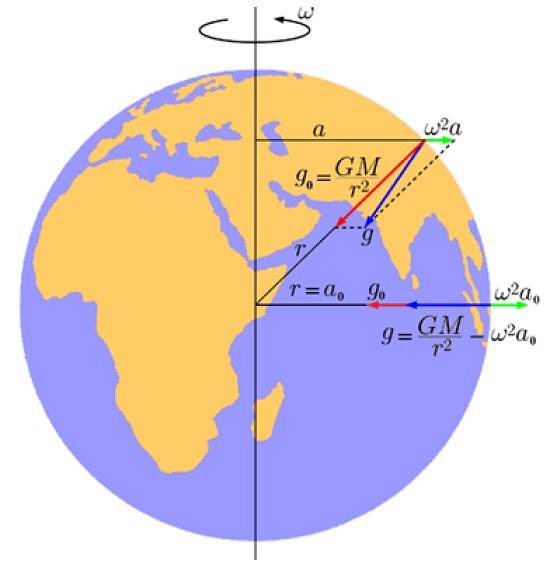
In questa equazione ω è la velocità angolare di rotazione della Terra e per è la distanza tra il punto sulla Terra, a una certa latitudine, e l'asse.
E in rosso è il componente dovuto all'attrazione gravitazionale planetaria:
go = GM / rDue
Di conseguenza, aggiungendo il vettore go + gl, si verifica un'accelerazione risultante g (in blu) che è la vera accelerazione di gravità della Terra (o accelerazione effettiva) e che come vediamo non punta esattamente al centro.
Inoltre, la componente laterale dipende dalla latitudine: è zero ai poli e quindi il campo gravitazionale è massimo lì. All'equatore si oppone all'attrazione gravitazionale, riducendo la gravità effettiva, la cui grandezza rimane:
g = GM / rDue - ωDueR
Con R = raggio equatoriale della Terra.
È ormai chiaro che le superfici equipotenziali della Terra non sono sferiche, ma assumono una forma tale g essere sempre perpendicolari a loro in tutti i punti.
Differenze tra geoide ed ellissoide
Ecco il secondo fattore che influenza la variazione del campo gravitazionale terrestre: le variazioni locali di gravità. Ci sono luoghi in cui la gravità aumenta perché c'è più massa, ad esempio sulla collina nella figura a).
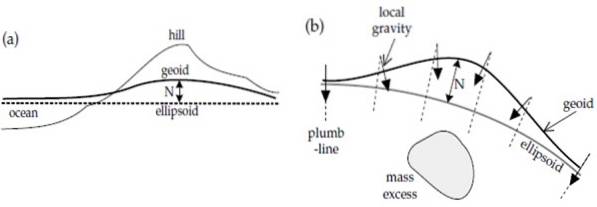
Oppure c'è un accumulo o un eccesso di massa sotto la superficie, come in b). In entrambi i casi c'è un'elevazione nel geoide perché maggiore è la massa, maggiore è l'intensità del campo gravitazionale..
D'altra parte, sopra l'oceano, la densità è inferiore e di conseguenza il geoide sprofonda, come vediamo a sinistra della figura a), sopra l'oceano..
Dalla figura b) si può anche vedere che la gravità locale, indicata con frecce, è sempre perpendicolare alla superficie del geoide, come abbiamo detto. Ciò non accade sempre con l'ellissoide di riferimento.
Le ondulazioni del geoide
La figura indica anche, con una freccia bidirezionale, il dislivello tra il geoide e l'ellissoide, che viene chiamato ondulazione y è indicato come N. Le ondulazioni positive sono correlate alla massa in eccesso e le ondulazioni negative ai difetti.
Le ondulazioni non superano quasi mai i 200 m. In realtà, i valori dipendono da come viene scelto il livello del mare che funge da riferimento, poiché alcuni paesi scelgono in modo diverso in base alle loro caratteristiche regionali.
Vantaggi di rappresentare la Terra come un geoide
-Sul geoide il potenziale effettivo, risultato del potenziale dovuto alla gravità e al potenziale centrifugo, è costante.
-La forza di gravità agisce sempre perpendicolare al geoide e l'orizzonte è sempre tangente ad esso.
-Il geoide offre un riferimento per applicazioni di mappatura ad alta precisione.
-Utilizzando il geoide, i sismologi possono rilevare la profondità alla quale si verificano i terremoti.
-Il posizionamento del GPS dipende dal geoide da utilizzare come riferimento.
-Anche la superficie dell'oceano è parallela al geoide.
-I prospetti e le discese del geoide indicano gli eccessi o difetti di massa, che sono i anomalie gravimetriche. Quando viene rilevata un'anomalia e in base al suo valore, è possibile inferire la struttura geologica del sottosuolo, almeno a determinate profondità..
Questo è il fondamento dei metodi gravimetrici in geofisica. Un'anomalia gravimetrica può indicare accumuli di determinati minerali, strutture sepolte nel sottosuolo o persino spazi vuoti. Le cupole saline nel sottosuolo, rilevabili con metodi gravimetrici, sono indicative in alcuni casi della presenza di olio.
Riferimenti
- QUELLA. Euronews. La presa della gravità sulla Terra. Estratto da: youtube.com.
- GIOIA. Geoide. Estratto da: youtube.com.
- Griem-Klee, S. Esplorazioni minerarie: gravimetria. Estratto da: geovirtual2.cl.
- Lowrie, W. 2007. Fondamenti di geofisica. 2 °. Edizione. Cambridge University Press.
- NOAA. Qual è il geoide? Estratto da: geodesy.noaa.gov.
- Sheriff, R. 1990. Applied Geophysics. 2 °. Edizione. Cambridge University Press.



Nessun utente ha ancora commentato questo articolo.