
Caratteristiche, vantaggi, svantaggi della proiezione conica cartografica
Il proiezione conica cartografica Si caratterizza per la proiezione dei punti di una superficie sferica sulla superficie di un cono, il cui vertice si trova sull'asse passante per i poli ed è tangente o secante alla sfera. Il cono è una superficie che può essere aperta in un piano, formando un settore angolare e senza deformare le linee proiettate su di esso.
Il matematico Johann Heinrich Lambert (1728 - 1777) è stato colui che ha ideato questa proiezione, che appare per la prima volta nel suo libro Prospettiva di Freye (1759), dove ha compilato varie teorie e riflessioni sulle proiezioni.
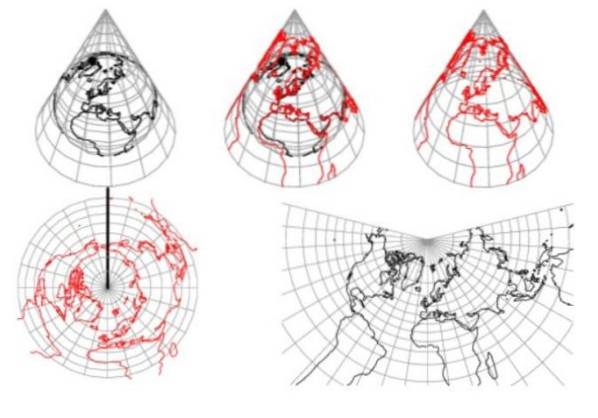
Nelle proiezioni coniche della superficie terrestre, i meridiani diventano linee radiali centrate sul vertice, con spaziatura angolare uguale, ei paralleli terrestri diventano archi circolari concentrici al vertice.
La figura 1 mostra che la proiezione conica non consente di rappresentare entrambi gli emisferi. Inoltre, si osserva chiaramente che le distanze sono distorte rispetto ai paralleli che intercettano il cono.
Per questi motivi, questo tipo di proiezione viene utilizzato per rappresentare regioni di media latitudine, estese da est a ovest e di minore estensione nord-sud. Questo è il caso degli Stati Uniti continentali.
Indice articolo
- 1 Vantaggi
- 1.1 La proiezione conica equidistante
- 2 Proiezione conica di Albert
- 3 Proiezione conica conforme di Lambert
- 4 Riferimenti
Vantaggio
La Terra può essere approssimata a una sfera con un raggio di 6378 km, considerando che tutte le masse di terra e d'acqua si trovano su quella grande sfera. Si tratta di convertire questa superficie, che copre un oggetto in tre dimensioni, come una sfera, in un altro oggetto in due dimensioni: una mappa piatta. Ciò comporta l'inconveniente che la superficie curva sia distorta, quando si vuole proiettarla sul piano.
Le proiezioni cartografiche, come la proiezione conica, cercano di risolvere questo problema con la minore perdita di precisione possibile. Quindi, ci sono diverse opzioni per fare una proiezione, a seconda delle caratteristiche che vuoi evidenziare..
Tra queste caratteristiche importanti ci sono le distanze, l'area della superficie, gli angoli e altro ancora. Il modo migliore per preservarli tutti è rappresentare la Terra in 3D in scala. Ma questo non è sempre pratico.
Portare un globo ovunque non è facile, poiché occupa volume. Né puoi vedere l'intera superficie della Terra in una volta, ed è impossibile riprodurre tutti i dettagli su un modello in scala..
Possiamo immaginare che il pianeta sia un'arancia, sbucciamo l'arancia e stendiamo la buccia sul tavolo, cercando di ricostruire l'immagine della superficie dell'arancia. È chiaro che molte informazioni andranno perse durante il processo.
Le opzioni di proiezione sono le seguenti:
- Proietta su un aereo o
- Su un cilindro, che può essere sviluppato come un piano rettangolare.
- Finalmente su un cono.
Il sistema di proiezione conica ha il vantaggio di essere esatto rispetto alle parallele scelte per intercettare il cono di proiezione..
Inoltre, mantiene praticamente intatto l'orientamento lungo i meridiani, sebbene possa distorcere leggermente la scala lungo i meridiani per latitudini lontane dai paralleli standard o di riferimento. Pertanto è opportuno rappresentare paesi o continenti molto grandi.
La proiezione conica equidistante
È il sistema di proiezione conico originariamente utilizzato da Tolomeo, un geografo greco vissuto tra il 100-170 d.C. Successivamente nel 1745 fu migliorata.
È usato frequentemente negli atlanti delle regioni con latitudini intermedie. È adatto per mostrare aree con pochi gradi di latitudine e che appartengono a uno degli emisferi equatoriali.
In questa proiezione le distanze sono vere lungo i meridiani e nei due paralleli standard, cioè i paralleli scelti per intercettare con il cono di proiezione..
Nella proiezione conica equidistante, un punto sulla sfera si estende radialmente fino alla sua intersezione con il cono tangente o secante, prendendo il centro della sfera come centro di proiezione.
Svantaggi
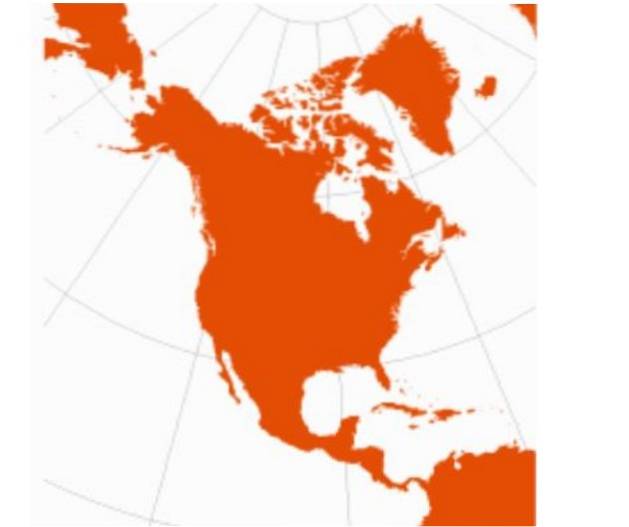
Il principale svantaggio della proiezione conica è che non è applicabile alle regioni equatoriali.
Inoltre, la proiezione conica non è appropriata per la mappatura di grandi regioni, ma piuttosto di aree particolari, come il Nord America..
Proiezione conica di Albert
Usa due paralleli standard e preserva l'area, ma non la scala e la forma. Questo tipo di proiezione conica fu introdotto da H. C. Albers nel 1805.
Tutte le aree sulla mappa sono proporzionali a quelle sulla Terra. In regioni limitate, le indicazioni stradali sono relativamente accurate. Le distanze corrispondono a quelle della superficie sferica sui paralleli standard.
Negli Stati Uniti questo sistema di proiezione viene utilizzato per mappe che mostrano i limiti degli stati dell'Unione, per i quali 29,5º N e 45,5º N sono scelti come paralleli standard, con un errore di scala massimo dell'1, 25%.
Le mappe realizzate con questa proiezione non conservano gli angoli corrispondenti a quelli della sfera, né preservano la prospettiva o l'equidistanza.
Proiezione conica conforme di Lambert
Fu proposto nel 1772 dall'omonimo matematico e geografo svizzero. La sua caratteristica principale è che utilizza un cono tangente o secante alla sfera e la proiezione mantiene invarianti gli angoli. Queste qualità lo rendono molto utile nelle carte di navigazione aeronautiche..
Lo United States Geological Survey (USGS) utilizza la proiezione conica di Lambert. In questa proiezione, le distanze sono vere lungo i paralleli standard.

Nella proiezione conica di Lambert le direzioni rimangono ragionevolmente precise. Le aree e le forme sono leggermente distorte in posizioni vicine ai paralleli standard, ma l'alterazione della forma e dell'area aumenta con la separazione da esse..
Poiché l'obiettivo di questa proiezione è di mantenere direzioni e angoli uguali a quelli originali sulla sfera o sull'ellissoide, non esiste un metodo geometrico per ottenerlo, a differenza della proiezione equidistante di Tolomeo..
Piuttosto è un metodo di proiezione analitico, basato su formule matematiche.
Le mappe di base USGS per i 48 stati continentali usano 33ºN e 45ºN come paralleli standard, producendo un errore massimo della mappa del 2,5%..
Per le carte nautiche in Alaska, i paralleli di base utilizzati sono 55ºN e 65ºN. Invece, l'atlante nazionale del Canada utilizza 49ºN e 77ºN.
Riferimenti
- Geohunter. La proiezione della conica conforme di Lambert. Estratto da: geo.hunter.cuny.edu
- Gisgeografia. Proiezione conica: Lambert, Albers e Polyconic. Estratto da: gisgeography.com
- Gisgeografia. Cosa sono le proiezioni cartografiche? Estratto da: gisgeography.com
- USGS. Proiezioni cartografiche. Estratto da: icsm.gov.au
- Weisstein, Eric W. "Proiezione conica di area uguale di Albers". Estratto da: mathworld.wolfram.com
- Weisstein, Eric W. "Conic Projection" Estratto da: mathworld.wolfram.com
- Weisstein, Eric W. "Lambert Conformal Conic Projection" Estratto da: mathworld.wolfram.com
- Wikipedia. Elenco delle proiezioni cartografiche. Estratto da: en.wikipedia.com



Nessun utente ha ancora commentato questo articolo.