
Caratteristiche, applicazioni ed esempi del processo politropico
UN processo politropico è un processo termodinamico che si verifica quando la relazione tra la pressione P e il volume V dato da P.Vn rimane costante. L'esponente n è un numero reale, generalmente compreso tra zero e infinito, ma in alcuni casi può essere negativo.
Il valore di n riceve il nome di indice di politropia ed è importante sottolineare che durante un processo termodinamico politropico detto indice deve mantenere un valore fisso, altrimenti il processo non sarà considerato politropico.

Indice articolo
- 1 Caratteristiche dei processi politropici
- 2 Applicazioni
- 2.1 Lavorare su processi politropici per diversi valori di n
- 3 Esempi di processi politropici
- 3.1 - Esempio 1
- 3.2 - Esempio 2
- 4 Riferimenti
Caratteristiche dei processi politropici
Alcuni casi caratteristici di processi politropici sono:
- Il processo isotermico (a temperatura T costante), in cui l'esponente è n = 1.
- Un processo isobarico (a pressione costante P), in questo caso n = 0.
- Il processo isocoro (a volume V costante), per il quale n = + ∞.
- Processi adiabatici (a entropia S costante), in cui l'esponente è n = γ, dove γ è la costante adiabatica. Questa costante è il quoziente tra la capacità termica a pressione costante Cp divisa per la capacità termica a volume costante Cv:
γ = Cp / Cv
- Qualsiasi altro processo termodinamico che non sia uno dei casi precedenti. ma questo è conforme P.Vn = ctte con indice politropico reale e costante n sarà anche un processo politropico.
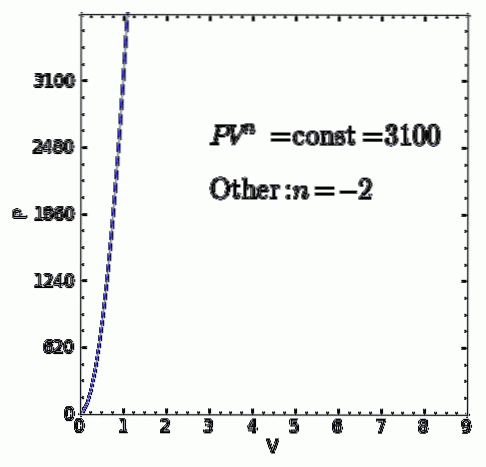
Applicazioni
Una delle principali applicazioni dell'equazione politropica è calcolare il lavoro svolto da un sistema termodinamico chiuso, quando passa da uno stato iniziale a uno stato finale in modo quasi statico, cioè seguendo una successione di stati di equilibrio.
Lavorare su processi politropici per diversi valori di n
Per n ≠ 1
Il lavoro meccanico W eseguito da un sistema termodinamico chiuso è calcolato dall'espressione:
W = ∫P.dV
Dove P è la pressione e V il volume.
Come nel caso di un processo politropico, la relazione tra pressione e volume è:
P.V n = costante = C
Risolvendo per P dall'espressione precedente per sostituirlo nell'espressione di lavoro:
P = C /V n
Abbiamo il lavoro meccanico eseguito durante un processo politropico, che inizia in uno stato iniziale 1 e termina nello stato finale 2. Tutto questo appare nella seguente espressione:


C = P1 V1n = PDue VDuen
Sostituendo il valore della costante nell'espressione di lavoro, si ottiene:
W = (PDue VDue - P1 V1) / (1-n)
Nel caso in cui la sostanza di lavoro possa essere modellata come un gas ideale, abbiamo la seguente equazione di stato:
P.V = m.R.T
Dove m è il numero di moli del gas ideale e R è la costante universale dei gas.
Per un gas ideale che segue un processo politropico con indice di politropia diverso dall'unità e che passa da uno stato con temperatura iniziale T1 ad un altro stato con temperatura TDue abbiamo che il lavoro svolto è dato dalla seguente formula:
W = m R (TDue - T1) / (1-n)
Per n → ∞
Secondo la formula per il lavoro ottenuto nella sezione precedente, abbiamo che il lavoro di un processo politropico con n = ∞ è nullo, perché l'espressione dell'opera è divisa per infinito e quindi il risultato tende a zero.
Un altro modo per arrivare a questo risultato è dalla relazione P1 V1n = PDue VDuen, che può essere riscritto come segue:
(P1/ PDue) = (VDue/ V1)n
Prendendo l'ennesima radice in ogni membro, otteniamo:
(VDue/ V1) = (P1/ PDue)(1 / n)
Nel caso in cui n → ∞, abbiamo (VDue/ V1) = 1, il che significa che:
VDue = V1
Cioè, il volume non cambia in un processo politropico con n → ∞. Pertanto, il differenziale di volume dV nell'integrale del lavoro meccanico è 0. Questi tipi di processi politropici sono anche noti come processi isocorico, o processi a volume costante.
Per n = 1
Ancora una volta abbiamo l'espressione l'espressione per lavoro:
W = ∫P dV
Nel caso di un processo politropico con n = 1, la relazione tra pressione e volume è:
P V = costante = C
Risolvendo per P dall'espressione precedente e sostituendo, abbiamo il lavoro fatto per passare dallo stato iniziale 1 allo stato finale 2:

Vale a dire:
W = C ln (VDue/ V1).
Poiché gli stati iniziale e finale sono ben determinati, così sarà il ctte. Vale a dire:
C = P1 V1 = PDue VDue
Infine, abbiamo le seguenti espressioni utili per trovare il lavoro meccanico di un sistema chiuso politropico in cui n = 1.
W = P1 V1 ln (VDue/ V1) = PDue VDue ln (VDue/ V1)
Se la sostanza di lavoro è costituita da m moli di gas ideale, è possibile applicare l'equazione di stato del gas ideale: P V = m.R.T.
In questo caso, come P.V1 = ctte, abbiamo che un processo politropico con n = 1 è un processo a temperatura costante T (isotermica), per cui si possono ottenere le seguenti espressioni per il lavoro:
W = m R T1 ln (VDue/ V1) = m R TDue ln (VDue/ V1)

Esempi di processi politropici
- Esempio 1
Supponiamo un cilindro con un pistone mobile riempito con un chilogrammo di aria. Inizialmente l'aria occupa un volume V1= 0,2 m3 ad una pressione P1= 400 kPa. Si segue un processo politropico con n = γ = 1.4, il cui stato finale ha pressione PDue = 100 kPa. Determina il lavoro svolto dall'aria sul pistone.
Soluzione
Quando l'indice di politropia è uguale alla costante adiabatica, c'è un processo in cui la sostanza di lavoro (aria) non scambia calore con l'ambiente, e quindi l'entropia non cambia..
Per l'aria, un gas ideale biatomico, abbiamo:
γ = Cp / Cv, con Cp = (7/2) R e Cv = (5/2) R
Poi:
γ = 7/5 = 1,4
Utilizzando l'espressione del processo politropico, il volume finale dell'aria può essere determinato:
VDue = [(PDue V11.4) / PDue](1 / 1,4) = 0,54 m3.
Ora abbiamo le condizioni per applicare la formula per il lavoro svolto in un processo politropico per n ≠ 1 ottenuta sopra:
W = (PDue VDue - P1 V1) / (1-n)
Sostituendo i valori appropriati abbiamo:
W = (100 kPa 0,54 m3 - 400 kPa 0,2 m3) / (1 - 1,4) = 65,4 kJ
- Esempio 2
Supponiamo lo stesso cilindro dell'esempio 1, con un pistone mobile riempito con un chilogrammo di aria. Inizialmente l'aria occupa un volume V1 = 0,2 m3 ad una pressione P1 = 400 kPa. Ma a differenza del caso precedente, l'aria si espande isotermicamente per raggiungere una pressione finale P2 = 100 kPa. Determina il lavoro svolto dall'aria sul pistone.
Soluzione
Come visto in precedenza, i processi isotermici sono processi politropici con indice n = 1, quindi è vero che:
P1 V1 = P2 V2
In questo modo il volume finale può essere facilmente sfogliato per ottenere:
V2 = 0,8 m3
Quindi, usando l'espressione di lavoro ottenuta in precedenza per il caso n = 1, abbiamo che il lavoro svolto dall'aria sul pistone in questo processo è:
W = P1 V1 ln (V2 / V1) = 400000 Pa × 0,2 m3 ln (0,8 / 0,2) = 110,9 kJ.
Riferimenti
- Bauer, W. 2011. Fisica per l'ingegneria e le scienze. Volume 1. Mc Graw Hill.
- Cengel, Y. 2012. Termodinamica. 7a edizione. Mcgraw hill.
- Figueroa, D. (2005). Serie: Fisica per la scienza e l'ingegneria. Volume 4. Fluidi e termodinamica. A cura di Douglas Figueroa (USB).
- López, C. La prima legge della termodinamica. Estratto da: culturacientifica.com.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Serway, R., Vulle, C. 2011. Fondamenti di fisica. 9 ° Ed. Cengage Learning.
- Università di Siviglia. Macchine termiche. Recupero da: laplace.us.es.
- Wikiwand. Processo politropico. Estratto da: wikiwand.com.


Nessun utente ha ancora commentato questo articolo.