
Spiegazione della prima condizione di equilibrio, esempi, esercizi
Il prima condizione di equilibrio richiede che la somma vettoriale di tutte le forze agenti su un corpo sia zero, in modo che sia a riposo (equilibrio statico) o con moto rettilineo uniforme (equilibrio dinamico).
Questa somma di forze non è altro che la forza netta che agisce sul corpo, espressa matematicamente in questo modo:
Fnetto = 0
∑ F = 0

Nello spazio, la prima condizione di equilibrio dà origine a tre equazioni, una per ogni dimensione:
∑ FX = 0; ∑ FY = 0 e ∑ Fz = 0
Quando queste equazioni sono soddisfatte, l'oggetto non si traduce o, se lo fa, sarà a velocità costante.
Guardandoci intorno ci rendiamo conto che cerchiamo continuamente di soddisfare la prima condizione di equilibrio affinché le cose non cadano.
Pertanto, cerca di compensare l'attrazione gravitazionale della Terra per mezzo di supporti, funi o supporti di alcuni, in modo che in questo modo le cose rimangano al loro posto e non finiscano a terra..
Altre volte ciò che è necessario è impedire che i campi elettromagnetici esterni interferiscano con il funzionamento dei circuiti elettrici e dei dispositivi di comunicazione. In questo caso, sono le cariche elettriche che devono essere in equilibrio..
Indice articolo
- 1 Esempi
- 1.1 Edifici
- 1.2 Semafori e cartelli appesi
- 1.3 Conduttori in equilibrio elettrostatico
- 1.4 Lampade da soffitto
- 1.5 Libri e oggetti sui tavoli
- 1.6 Misura della viscosità di un liquido
- 2 passaggi per applicare la prima condizione di equilibrio
- 3 esercizi risolti
- 3.1 - Esercizio risolto 1
- 3.2 - Esercizio risolto 2
- 4 Argomenti di interesse
- 5 Riferimenti
Esempi
Un gran numero di oggetti di uso quotidiano soddisfano la prima condizione di equilibrio, si tratta di osservare attentamente:
Edifici
I costruttori cercano stabilità nelle costruzioni in modo che gli utenti rimangano al sicuro. L'obiettivo della statica è studiare le condizioni per l'equilibrio statico che si verifica in edifici, ponti, strade e tutti i tipi di strutture..
Semafori e cartelli appesi
Questi dispositivi di segnalazione devono rimanere fissi per adempiere alle loro funzioni, pertanto sono trattenuti da cavi, pali e aste in modo tale da soddisfare la prima condizione di equilibrio..

Conduttori in equilibrio elettrostaticoattico
Quando i materiali conduttivi come il rame e altri metalli acquisiscono una carica elettrica, viene presto stabilito l'equilibrio elettrostatico, lasciando la carica in eccesso sulla superficie conduttiva. All'interno del campo elettrico è zero.
Questo effetto viene spesso utilizzato per isolare apparecchiature elettriche ed elettroniche da campi esterni, utilizzando la cosiddetta gabbia di Faraday. La gabbia è realizzata in materiale conduttivo e circonda l'apparecchiatura da proteggere.
Durante i temporali, le automobili fungono da gabbie di Faraday proteggendo gli occupanti dalle scosse elettriche..
Lampade da soffitto
Nei sistemi di illuminazione, come le lampade a sospensione, la prima condizione di equilibrio è utilizzata per fissarli a soffitto, pavimento o parete.

Libri e oggetti sui tavoli
Gli oggetti posti su tavoli e mensole soddisfano la prima condizione di equilibrio. La forza normale che il supporto esercita sugli oggetti è responsabile della compensazione del peso.
Misura della viscosità di un liquido
Per determinare la viscosità di un liquido, un oggetto sferico di diametro noto viene fatto cadere al suo interno e la sua velocità rallenterà a causa della resistenza. La velocità della sfera è costante, trovandosi così in equilibrio dinamico.
Maggiore è la viscosità del liquido, minore è la velocità con cui la sfera si muove all'interno.
Passaggi per applicare la prima condizione di equilibrio
-Crea un diagramma a corpo libero, mostrando tutte le forze che agiscono sul corpo (ometti quelle che il corpo esercita sugli altri).
-Selezionare un sistema di coordinate cartesiane, assicurandosi che, per quanto possibile, le forze si trovino su uno qualsiasi degli assi. La direzione positiva viene solitamente presa nella direzione del movimento o di un possibile movimento.
-Determina le componenti cartesiane di ciascuna forza.
-L'applicazione della seconda legge di Newton per ogni componente, stabilita all'inizio, rimane quindi un sistema di equazioni.
-Risolvi il sistema di equazioni sollevato nel passaggio precedente.
Esercizi risolti
- Risolto esercizio 1
Il blocco della figura, della massa m, si muove in discesa sul piano inclinato ad angolo θ con velocità costante. Calcola il valore del coefficiente di attrito cinetico μK, se la massa del blocco è m = 5 kg e θ = 37º.

Soluzione
Il primo passo è disegnare il diagramma del corpo libero e scegliere un sistema di coordinate cartesiane per esprimere ogni forza in modo vettoriale. Le forze che agiscono sul blocco sono:
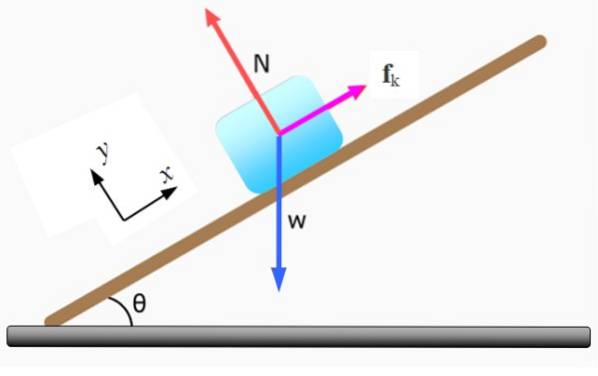
-Il normale N esercitato dal piano inclinato, è perpendicolare alla superficie di questo.
-Il peso W è diretto verticalmente verso il basso.
-Attrito cinetico FK che è contrario al movimento. Se non esistesse, il corpo si muoverebbe in discesa con un'accelerazione pari a g.senθ.
Come il peso W è inclinato rispetto agli assi coordinati selezionati, deve essere scomposto nelle sue componenti cartesiane:
WX = mg sin 37º = 5 kg x 9,8 m / sDue x sin 37º = 29. 5 N
WY = mg.cos 37º = 5 kg x 9,8 m / sDue x cos 37º = 39,1 N
Viene ora applicata la seconda legge di Newton, impostando ogni somma a 0, poiché il blocco manca di accelerazione quando si muove a velocità costante:
∑ FY = N - WY = 0
∑ FX = WX - FK = 0
L'entità dell'attrito cinetico è proporzionale all'entità della normale, il coefficiente di attrito cinetico è μK la costante della proporzionalità.
FK = μK N
Allo stesso tempo:
N = WY = 39,1 N
Più:
FK = WX
Perciò:
- 5 N = μK x 39,1 N
μK = 29,5 / 39,1 = 0,75
- Esercizio risolto 2
Calcola l'entità delle sollecitazioni che supportano il semaforo di massa 33 kg, mostrato in figura:
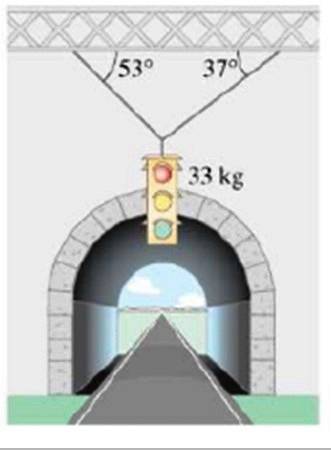
Soluzione
Lo schema a corpo libero è realizzato sia per il semaforo che per il nodo che tiene i cavi:
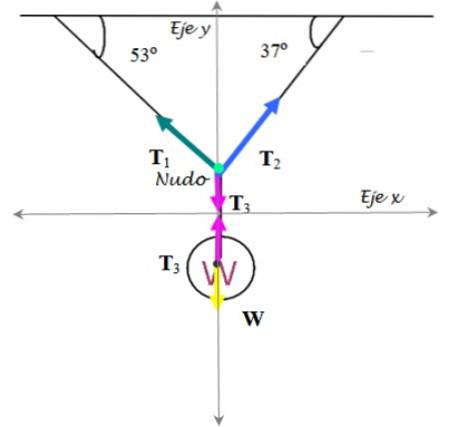
Semaforo
Su di esso agisce: la tensione T3 su e il peso W. giù. Perciò:
∑ FY = W - T3 = 0
Perciò:
T3 = 33 kg x 9,8 m / sDue = 323,4 N
Nodo
Le tensioni vengono scomposte nelle loro componenti cartesiane:
∑ FY = T1 sin 53º + TDue sen 37º - T3 = 0
∑ FX = TDue cos 37º - T1 cos 53º = 0
E il seguente sistema di equazioni lineari si ottiene con due incognite T1 e TDue :
- 0,6 T1 + 0,8 TDue = 0
0,8 T1 + 0,6 TDue = 323,4
La soluzione di questo sistema di equazioni è: T1 = 258,7 N e TDue = 194,0 N
Temi di interesse
Condizioni di equilibrio.
Seconda condizione di equilibrio.
Riferimenti
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
- Figueroa, D. (2005). Serie: Fisica per la scienza e l'ingegneria. Volume 4. Sistemi di particelle. A cura di Douglas Figueroa (USB).
- Giancoli, D. 2006. Fisica: principi con applicazioni. 6 °. Ed prentice hall.
- Sears, Zemansky. 2016. Fisica universitaria con fisica moderna. 14th. Ed. Volume 1.
- Wikipedia. Statico (meccanico). Estratto da: es.wikipedia.org.


Nessun utente ha ancora commentato questo articolo.