
Calcolo del peso (fisico), unità, esempi, esercizi

Il peso è la forza con cui la Terra attira gli oggetti sulla sua superficie. Ogni volta che un oggetto cade, cade a terra, non è in grado di arrampicarsi da solo, né è senza peso a metà strada, perché la Terra lo attrae..
Tutti gli oggetti invariabilmente si attraggono l'un l'altro, anche i più piccoli, solo l'entità della forza con cui lo fanno è proporzionale alla massa. Ciò significa che gli oggetti di piccola massa esercitano poca forza sugli altri, ma i corpi celesti come la Terra sono in grado di esercitare una forza molto grande..
La Terra mantiene la Luna in orbita attorno ad essa grazie a questa forza attrattiva, che viene chiamata attrazione gravitazionale quando si tratta di oggetti lontani dalla superficie terrestre, e peso quando gli oggetti sono vicini.
Da ciò ne consegue che la forza di gravità non richiede che gli oggetti siano necessariamente in contatto tra loro per poter agire: ecco perché si dice che sia una forza di azione a distanza.
Gli oggetti continuano ad avere un peso anche se si trovano ad una certa altezza dal suolo e più sono massicci, maggiore sarà questo peso.
Il grande scienziato inglese Isaac Newton è stato il primo a dare una spiegazione a questa questione, attraverso la legge universale di gravitazione che porta il suo nome e che da allora è servita a capire come interagiscono gli oggetti con la massa. Questo è molto importante, poiché qualsiasi oggetto sul pianeta ha un peso.
Indice articolo
- 1 unità di peso
- 1.1 Il chilogrammo-forza
- 1.2 La libbra-forza
- 2 Calcolo e formula del peso
- 3 Peso come vettore
- 4 Differenze tra peso, massa e volume
- 5 Esempi di peso
- 6 Esercizio risolto
- 7 Riferimenti
Unità di peso
Il Sistema Internazionale di unità SI ha come unità di peso il Newton, prende il nome da Isaac Newton. Questa è l'unità per misurare le forze di tutti i tipi.
Il newton, abbreviato N, è definito come la forza necessaria ad un oggetto con una massa di 1kg per acquisire un'accelerazione di 1m / sDue. Oltre al newton, ci sono altre unità di forza di uso comune, ad esempio le seguenti:
Il chilogrammo-forza
Il chilogrammo-forza o kilopond, abbreviato kg-f o kp, sebbene comunemente chiamato kg senza di più, è la forza che la Terra esercita su un oggetto che si trova al livello del mare ea 45º di latitudine nord. È necessario specificare la posizione, poiché come detto, il campo gravitazionale subisce variazioni con l'altezza e la latitudine.
Quando qualcuno dice che pesa 45 kg, ciò che realmente intende è che il suo peso è di 45 kg-f, perché il chilogrammo è l'unità riservata alla massa.
L'equivalenza tra kg-f e N è: 1kg-f = 9,8 N
Libbra-forza
Il libbra-forza, l'abbreviazione lb-f è anche un'unità di forza analoga a kg-f, poiché è la forza che la Terra esercita su un oggetto di 1 libbra di massa. E come con il kg-f, non ci sono problemi con i valori quando sei sulla Terra, cioè un oggetto di massa l lb, pesa 1 lb-f.
L'equivalenza in lb-f e N è: 1 lb-f ≡ 4,448222 N.
Calcolo e formula del peso
Il peso di un oggetto è proporzionale alla sua massa. Maggiore è la massa, maggiore è il peso.
La formula per trovare l'ampiezza del peso P (o anche W, come talvolta viene indicato, con "Peso" in inglese) è molto semplice:
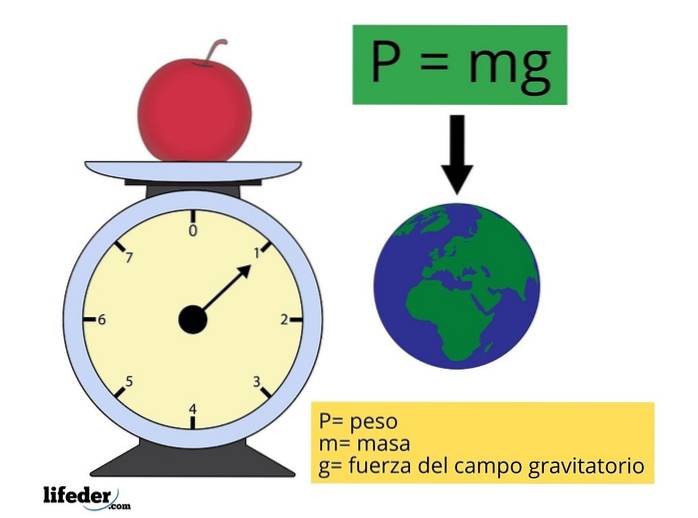
P = mg
Dove m rappresenta la massa dell'oggetto e g è l'ampiezza dell'accelerazione di gravità (intensità del campo gravitazionale o gravità), approssimativamente costante e il cui valore è preso come 9,81 m / sDue per i calcoli più frequenti.
Il peso è un vettore e le lettere in grassetto vengono utilizzate per distinguere tra un vettore e la sua grandezza. In questo modo quando si parla di P si capisce che è il valore numerico e quando si scrive P si fa riferimento al vettore:
P = m ∙g
Il g in grassetto è il campo gravitazionale della Terra, cioè l'influenza che la Terra esercita sullo spazio che la circonda, indipendentemente dal fatto che ci sia o meno un altro corpo che la percepisce. Ogni oggetto con massa ha il suo campo gravitazionale, piccolo o grande che sia.
L'intensità del campo gravitazionale terrestre g non è del tutto costante. Ha piccole variazioni che sorgono principalmente perché la Terra non è una sfera perfetta e anche a causa di differenze locali di altezza e densità. Ma per la maggior parte delle applicazioni, il valore è di 9,81 m / sDue Funziona molto bene.
Altri corpi celesti hanno il loro campo gravitazionale caratteristico, quindi l'accelerazione di gravità varia a seconda del pianeta o del satellite. Lo stesso oggetto avrebbe in ciascuno un peso diverso, quindi il peso non è una proprietà caratteristica delle cose, ma della materia in generale..
Peso come vettore
Il peso è un vettore e quindi ha grandezza, direzione e senso. In prossimità della superficie terrestre, il peso è un vettore in direzione verticale e la direzione è sempre verso il basso.
Di solito la direzione verticale è denominata come asse Y o z, e alla direzione verso il basso è assegnato un segno + o - per distinguerla dalla direzione verso l'alto. La scelta dipende dalla posizione dell'origine. Nell'immagine sotto, l'origine è stata scelta nel punto da cui cade la mela:
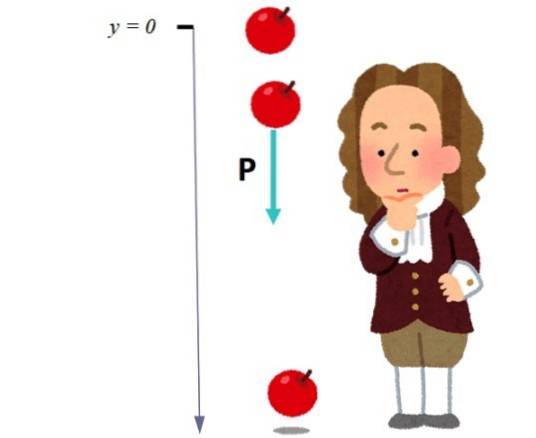
Il vettore unitario j, un vettore di grandezza uguale a 1, viene utilizzato per marcare e distinguere la direzione verticale. In termini di questo vettore, il peso è scritto in questo modo:
P = mg (- j)
Dove il segno negativo è assegnato alla direzione verso il basso.
Differenze tra peso, massa e volume

Questi tre concetti sono spesso confusi, ma rivedendo le caratteristiche del peso, è facile differenziarlo da massa e volume..
Per cominciare, il peso dipende dal campo gravitazionale in cui si trova l'oggetto. Ad esempio, sulla Terra e sulla Luna la stessa cosa ha un peso diverso, sebbene il numero di atomi che la compongono rimanga costante..
La massa è una quantità scalare, correlata al numero di atomi che compongono l'oggetto ed è evidenziata dalla resistenza che ha l'oggetto a cambiare il suo movimento, una proprietà chiamata inerzia.
Da parte sua, il volume è la misura dello spazio che occupa un oggetto, un'altra quantità scalare. Due oggetti con lo stesso volume non pesano lo stesso, ad esempio un cubo di ferro pesa molto di più di un cubo di polistirolo delle stesse dimensioni.
In sintesi:
- La massa è correlata alla quantità di materia che ha un corpo.
- Il peso è la forza esercitata dalla Terra su questa massa, proporzionale ad essa.
- Il volume è lo spazio occupato dalla materia.
Va notato che essendo quantità scalari, né la massa né il volume hanno direzione o senso, ma solo valore numerico e un'unità adeguata. D'altra parte, il peso, essendo un vettore, deve essere sempre espresso correttamente indicando la grandezza, l'unità, la direzione e il senso, come nel paragrafo precedente.
Esempi di peso
Tutti gli oggetti sulla Terra hanno un peso, puoi anche "pesare" oggetti che non sono sulla Terra, come altri pianeti o il Sole, anche se con mezzi indiretti, ovviamente.
Poiché la gamma di pesi è molto ampia, la notazione scientifica (in potenze di 10) viene utilizzata per esprimere alcuni che sono molto grandi o molto piccoli:
-Il sole: 1.989 × 1030 kg-f
-Giove: 1.898 × 1027 kg-f
-Una zanzara: 2.0 × 10-5 N
-Neonati: 34,3 N
-Un bambino: 353 N
-Persona adulta: 65 kg-f
-Un elefante adulto: 5,5 × 103 kg-f
-Balenottera azzurra: 1.0 × 106 N
Esercizio risolto
Una scatola di 20 kg di massa poggia su un tavolo.
a) Trova il peso della scatola e la forza normale che il tavolo esercita su di essa.
b) Un'altra scatola da 10 kg viene posizionata sopra la prima. Trova la normale che la tavola esercita sulla scatola da 20 kg e la normale che questa esercita sulla scatola più piccola.
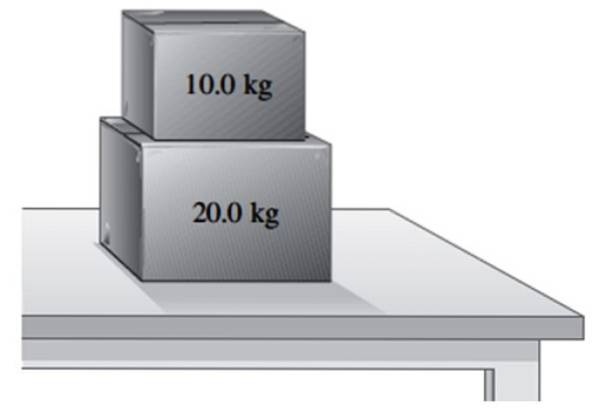
Soluzione a
È conveniente creare un diagramma del corpo libero sulla scatola, che consiste nel disegnare le forze che agiscono su di esso.
In questa situazione, la scatola più piccola non è ancora in cima, quindi ci sono solo due forze: la prima è il peso. P che si disegna verticalmente verso il basso, come indicato nelle sezioni precedenti e poi c'è la normale N, che è la forza perpendicolare esercitata dal tavolo e impedisce la caduta della scatola.
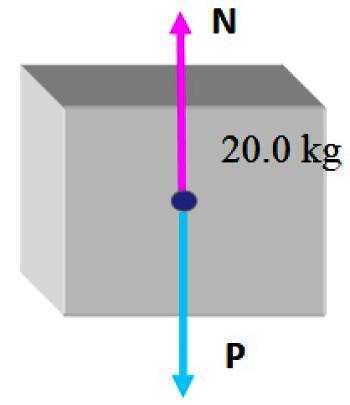
Dato che la scatola è in equilibrio statico in queste circostanze, è ragionevole concludere che l'ampiezza della normale è uguale a quella del peso, in modo che possa compensare, quindi:
N = mg = 20,0 kg x 9,8 m / sDue = 196 N; diretto verticalmente verso l'alto.
Da parte sua, il peso è P = 196 N diretto verticalmente verso il basso.
Soluzione b
Ora vengono creati nuovi diagrammi a corpo libero su entrambi gli oggetti. Per la scatola grande le cose cambiano un po ', poiché la scatola piccola esercita una forza su di essa.
Le forze sono le seguenti: N Y P sono rispettivamente la normale esercitata dalla tavola e il peso sulla scatola di 20,0 kg, che non è variato. E la nuova forza esercitata dalla piccola scatola è N1, il normale dovuto al contatto con la faccia superiore della scatola grande.
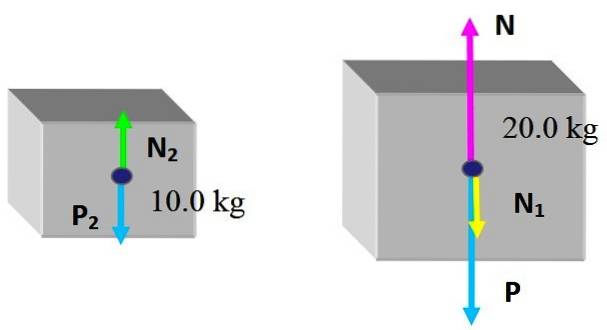
Per quanto riguarda la piccola scatola, riceve la normale NDue, esercitato dalla faccia superiore della grande scatola e ovviamente dal suo peso PDue. Poiché le scatole sono in equilibrio statico:
NDue - PDue = 0
N - N1 - P = 0
Dalla prima equazione abbiamo che NDue = PDue = 10 kg x 9,8 m / sDue = 98 N. Per legge di azione e reazione, l'entità della forza che riceve la scatola piccola è la stessa che esercita sulla scatola grande, quindi:
NDue = N1 = 98 N
Dalla seconda equazione, viene cancellata la normale N esercitata dalla tabella sul riquadro grande, che a sua volta ha il riquadro piccolo in alto:
N = N1 + P = 98 N + 196 N = 294 N
Riferimenti
- Figueroa, D. 2005. Serie: Fisica per le scienze e l'ingegneria. Volume 2. Dinamica. A cura di Douglas Figueroa (USB).
- Giambattista, A. 2010. Fisica. 2 °. Ed. McGraw Hill.
- Giancoli, D. 2006. Fisica: principi con applicazioni. 6 °. Ed prentice hall.
- Sears, Zemansky. 2016. Fisica universitaria con fisica moderna. 14th. Ed. Volume 1. Pearson.
- Serway, R., Jewett, J. 2008. Fisica per la scienza e l'ingegneria. Volume 1. 7th. Ed. Cengage Learning.
- Thomas Griffith, W. 2007. Fisica concettuale. Mc Graw Hill.


Nessun utente ha ancora commentato questo articolo.