
Concetto, tipi ed esempi di onde tridimensionali
Sono onde tridimensionali quelli che si propagano nello spazio, ad esempio l'onda sonora prodotta da un altoparlante. Quest'onda si propaga in tutte le direzioni, sebbene non con la stessa intensità in tutte..
Se un disturbo si verifica in un punto dello spazio, allora si propaga nelle tre direzioni spaziali, essendo i fronti d'onda superfici chiuse, sferiche, ellittiche o di altro tipo..

Se invece il luogo di origine delle onde, cioè la sorgente, ha una distribuzione piatta, allora il disturbo viaggerà principalmente nella direzione perpendicolare a detto piano, formando fronti d'onda piatti..
Indice articolo
- 1 Tipi di onde tridimensionali
- 1.1 Onde piane
- 1.2 Onde cilindriche
- 1.3 Onde sferiche
- 2 Intensità ed energia di un'onda sferica
- 3 Esempi di onde tridimensionali
- 3.1 Antenne che emettono onde elettromagnetiche
- 3.2 Onde sismiche
- 3.3 Il suono
- 4 Riferimenti
Tipi di onde tridimensionali
Nelle onde tridimensionali, i fronti d'onda sono un insieme di superfici immerse nello spazio tridimensionale.
Ora, il fronte d'onda è il luogo dei punti nello spazio che vengono raggiunti dal disturbo iniziale, nello stesso istante di tempo..
Di solito si considerano tre tipi di onde che viaggiano nello spazio tridimensionale, secondo la simmetria del fronte d'onda: onde piane, onde cilindriche e onde sferiche. Tuttavia, le onde reali non appartengono sempre a questi tipi, perché non hanno un grado di simmetria così elevato.
Onde piatte
Un'onda piana che viaggia nella direzione positiva x con velocità v è rappresentata funzionalmente come:
g (x, t) = f (x - v⋅t)
Questa onda non è limitata all'asse X, si estende anche nelle direzioni Y Y z. Ma la forma funzionale ci dice che tutti i punti che hanno la stessa coordinata x, indipendentemente dalle coordinate (z, y), hanno lo stesso valore g.
In questo caso i fronti d'onda sono piani paralleli al piano z-y che avanzano rapidamente v, il che significa che l'onda piana occupa tutto lo spazio tridimensionale.
L'espressione che rappresenta un'onda piana che si propaga in qualsiasi direzione o velocemente v, dove o rappresenta un vettore unitario di coseni direttori cos (α), cos (β) Y cos (γ), è:
g = f (û • r - v⋅t) = f (x cos (α) + y cos (β) + z cos (γ) - v⋅t)
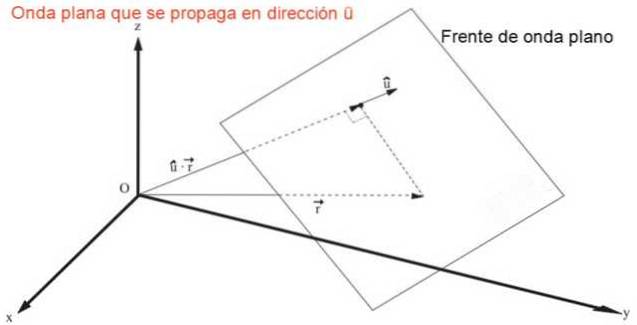
È facile mostrare, per sostituzione diretta, che l'espressione precedente è una soluzione dell'equazione delle onde tridimensionali, un'equazione in derivate parziali del secondo ordine lineare:
∂xxg + ∂yyg + ∂zzg = (1 / vDue) ∂ttg
L'equazione precedente può essere scritta in modo più compatto utilizzando l'operatore laplaciano ∇Due:
∇Dueg = (1 / vDue) ∂ttg
Onde cilindriche
Quando il disturbo iniziale è distribuito su una linea retta, allora l'onda si propaga in direzione radiale perpendicolare a quella linea, riempiendo lo spazio tridimensionale che la circonda, con fronti d'onda cilindrici..
Onde sferiche
Quando la sorgente è puntuale e il mezzo in cui si propaga l'onda tridimensionale è omogeneo e isotropo (le sue proprietà non cambiano a seconda della direzione), allora i fronti d'onda sono sfere concentriche al punto in cui si è verificato il disturbo iniziale..
Nel caso di un'onda sferica in cui l'intensità dell'onda è identica in tutte le direzioni, la funzione che descrive il disturbo dipende solo dalla distanza r alla sorgente puntiforme e all'ora t.
In questo caso abbiamo che il corrispondente laplaciano è:
∇Dueg = (1 / rDue) ∂r(rDue ∂rg)
Essendo l'equazione delle onde:
∇Dueg = (1 / vDue) ∂ttg
La soluzione generale sarebbe:
g (r, t) = (1 / r) F (r - v⋅t) + (1 / r) G (r + v⋅t)
In questo caso si dice che si tratta di un file onda sferica. Ma possono esserci delle varianti, come vedremo di seguito
Onde sferiche non isotropiche
Può anche accadere che un'onda sferica, cioè con i fronti d'onda formati da sfere concentriche ad un punto centrale, l'ampiezza o l'intensità dell'onda sia diversa nelle diverse direzioni..
Questo è ciò che accade quando la sorgente centrale dell'onda è più efficiente in una direzione rispetto ad altre..
Ad esempio, il suono prodotto da un altoparlante non ha la stessa intensità ovunque, anche in punti equidistanti dall'altoparlante..
L'intensità non è la stessa anche se il segnale impiega lo stesso tempo per raggiungere questi punti. È un'onda sferica che ha un modello direzionale non sferico.
Hai anche onde sferiche nel caso di onde elettromagnetiche create da un'antenna, ma potrebbero non essere ugualmente forti in tutte le direzioni..

Terreno disomogeneo
Quando il mezzo è disomogeneo, la velocità di propagazione dell'onda è diversa nelle diverse direzioni.
Un esempio di mezzo disomogeneo è l'atmosfera in cui ci sono differenze di pressione con l'altezza e ci sono gradienti di temperatura. Un altro esempio sono gli strati della crosta terrestre, che differiscono per densità e modulo elastico..
La disomogeneità fa sì che i fronti d'onda originati da una sorgente puntiforme centrale non siano sfere concentriche, poiché la distanza percorsa dall'onda, nello stesso periodo di tempo, è diversa in ogni direzione..
Quindi abbiamo un'onda tridimensionale il cui fronte d'onda non è sferico.
Intensità ed energia di un'onda sferica
Possiamo scrivere l'espressione di un'onda armonica sferica come questa:
g (r, t) = (go / r) cos (k⋅r - ω⋅t)
Dove i fronti d'onda si propagano con velocità radiale pari a:
v = ω / k
E la sua ampiezza diminuisce con l'inverso della distanza r dalla sorgente puntiforme delle onde sferiche.
Le onde armoniche lo hanno densita 'energia (energia per unità di volume) ε dato da:
ε = ½ ρ ωDue (go / r)Due
In questa equazione:
-ρ ha unità di massa per unità di volume e rappresenta la densità del mezzo in cui si propaga un'onda sonora.
-go è l'ampiezza dello spostamento di un elemento del mezzo, ad esempio un fluido, dovuto all'onda di propagazione.
Si noti che, trattandosi di un'onda sferica, la densità di energia diminuisce con l'inverso del quadrato della distanza.
L'intensità dell'onda, cioè l'energia trasmessa per unità di tempo è:
I = v⋅ε
Come sempre, in pratica la grandezza più importante è la potenza trasmessa per unità di area alla distanza radiale. r:
P = v⋅ε = Io / rDue
Essere ioo = ½ ρ v ωDue goDue.
L'energia totale trasmessa per unità di tempo attraverso una sfera di raggio r è: P⋅4πrDue= 4π⋅Io, e come previsto non dipende dalla distanza radiale.
Esempi di onde tridimensionali
Le onde tridimensionali sono molto frequenti, quindi abbiamo:
Antenne che emettono onde elettromagnetiche

Coprono uno spettro molto ampio, dalle onde radio comprese tra centinaia di KHz e centinaia di MHz, alle onde emesse dall'antenna del Wifi dell'ordine dei GHz, che già rientra nella gamma delle microonde.
Sappiamo che le microonde, sebbene non siano radiazioni ionizzanti, sono in grado di aumentare la temperatura corporea perché contengono molta acqua.
Pertanto non è consigliabile avere l'antenna wi-fi vicino alla testa o al corpo. Basta allontanarsi un po ', poiché a doppia distanza, l'intensità è la quarta parte.
Onde sismiche
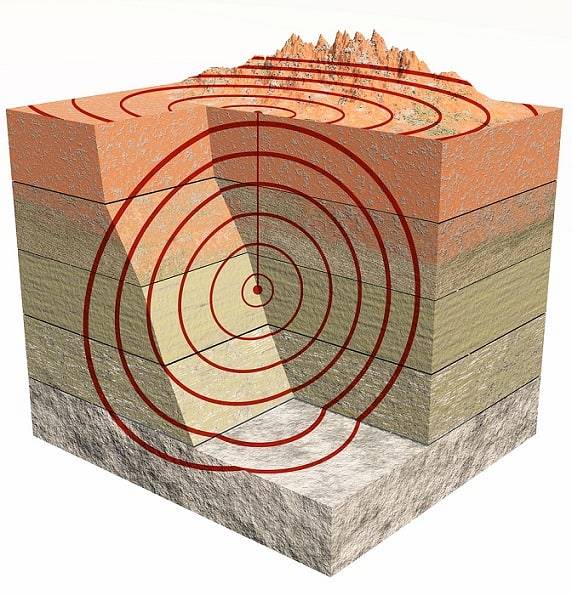
Sono anche onde tridimensionali. Principalmente ci sono i tipi P cosa sono le onde di compressione e quelle di tipo S quali sono il taglio o la cesoiatura (ssentire in inglese).
Le onde P o le primarie sono le prime ad arrivare perché si propagano più velocemente delle onde S o secondario.
Suono

Il suono è un tipo di onda tridimensionale. Queste onde si propagano in tutte le direzioni, anche se, come abbiamo detto prima, non con la stessa intensità in tutte le direzioni..
Questo perché la sorgente sonora non emette sempre una simmetria perfettamente sferica.
Riferimenti
- Baranek, L. 1969. Acustica. 2 °. Edizione. Mcgraw hill.
- Griffiths G. Onde lineari e non lineari. Estratto da: scholarpedia.org.
- Nottoli, H. 2004. Fisica applicata all'architettura. Nobuko.
- Whitham G.B. 1999. Onde lineari e non lineari. Wiley.
- Wikiwaves. Onde non lineari. Estratto da: wikiwaves.org



Nessun utente ha ancora commentato questo articolo.