
Esempi di metodo parallelogramma, esercizi risolti
Il metodo del parallelogramma è un metodo grafico per aggiungere due vettori nel piano. Viene spesso utilizzato per trovare la risultante di due forze applicate a un corpo o di due velocità, come nel caso di un nuotatore che intende attraversare un fiume perpendicolarmente e viene deviato dalla corrente.
Per costruire il parallelogramma, le origini dei vettori da sommare, disegnati in scala, devono coincidere in un punto.
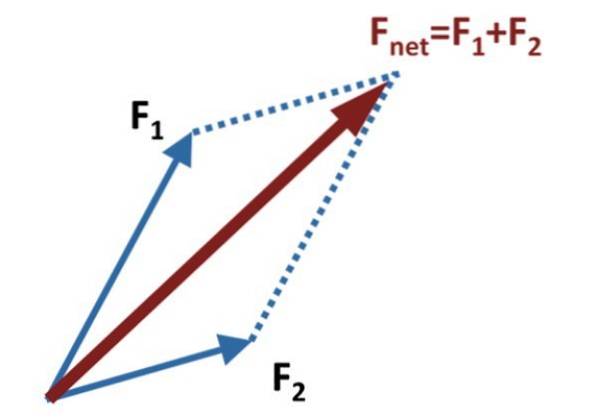
Quindi le linee ausiliarie vengono disegnate parallelamente a ciascun vettore, raggiungendo la fine dell'altro, come mostrato nella figura sopra.
La somma o il vettore risultante, chiamato anche forza netta, è il vettore Fnetto, che si ottiene disegnando il vettore che va dall'origine comune di F1 Y FDue, al punto in cui le linee parallele ausiliarie si intersecano. Nel diagramma della figura questi sono rappresentati da linee tratteggiate.
Il metodo prende il nome dalla figura che si forma con i vettori addendi e le linee ausiliarie, che è appunto un parallelogramma. La diagonale principale del parallelogramma è il vettore somma.
È molto importante notare che l'ordine in cui sono posizionati i vettori addendi non altera affatto la somma, poiché questa operazione tra i vettori è commutativa.
Indice articolo
- 1 Esempio del metodo del parallelogramma passo dopo passo
- 1.1 Caso speciale: somma di vettori perpendicolari
- 2 Esercizi risolti
- 2.1 - Esercizio 1
- 2.2 - Esercizio 2
- 3 Riferimenti
Esempio del metodo del parallelogramma passo dopo passo
L'immagine seguente mostra i vettori v Y o in unità arbitrarie. Il vettore v misura 3,61 unità e forma un angolo di 56,3º con l'orizzontale, mentre o misura 6,32 unità e un angolo di 18,4º rispetto a detta linea di riferimento.
Troveremo la sua somma vettoriale usando il metodo del parallelogramma.
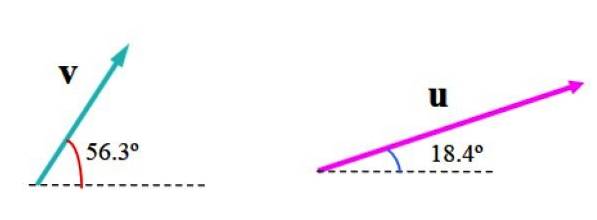
Scegli una scala appropriata, come quella mostrata nella figura seguente, in cui il piano è stato diviso da una griglia. La larghezza del quadrato rappresenta una (1) unità.
Poiché i vettori non vengono alterati durante la traslazione, sono posizionati in modo tale che le loro origini coincidano con l'origine del sistema di coordinate (immagine a sinistra).
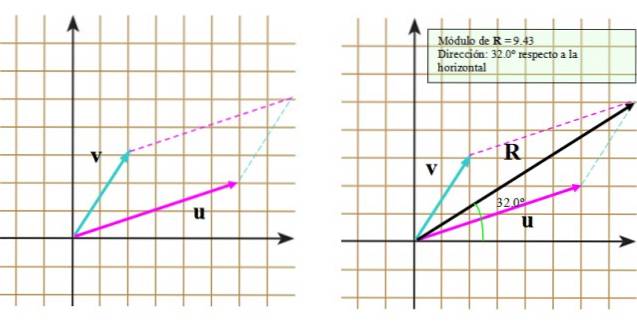
Ora seguiamo questi passaggi:
- Traccia alla fine del vettore v una linea segmentata parallela al vettore o.
- Ripeti la procedura ma questa volta con la fine del vettore o.
- Disegna la diagonale principale che si estende dall'origine comune al punto di intersezione delle linee segmentate.
Il risultato può essere visto nell'immagine a destra, in cui appare il vettore risultante R.
Se vogliamo conoscere l'entità di R, possiamo misurarne la lunghezza e confrontarla con la scala che abbiamo. E per quanto riguarda la sua direzione, l'asse orizzontale o l'asse verticale possono essere usati come riferimenti, per esempio.
Quando si utilizza l'asse orizzontale o l'asse x, l'angolo che R la forma con detto asse viene misurata con il goniometro e in questo modo si conosce la direzione di R.
Allo stesso modo, l'ampiezza e la direzione di R può essere calcolato utilizzando i teoremi del coseno e del seno, poiché il parallelogramma formato può essere diviso in due triangoli congruenti, i cui lati sono i moduli dei vettori o, v Y R. Vedi esempio lavorato 1.
Caso speciale: somma di vettori perpendicolari
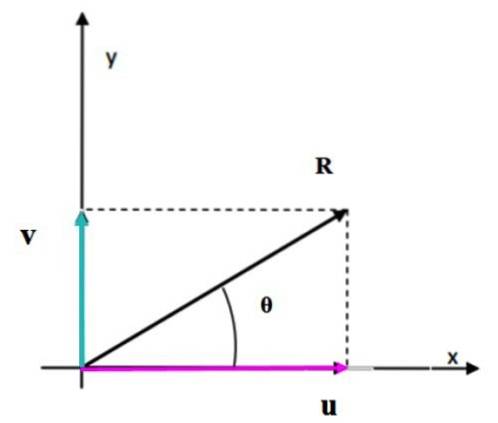
Quando i vettori sono perpendicolari tra loro, la figura che si forma è un rettangolo. Il modulo del vettore risultante corrisponde alla lunghezza della diagonale, che può essere facilmente calcolata utilizzando il teorema di Pitagora.
Esercizi risolti
- Esercizio 1
Abbiamo il vettore v, che misura 3,61 unità e forma un angolo di 56,3º con l'orizzontale e il vettore o, la cui misura è di 6,32 unità e forma un angolo di 18,4º (figura 2). Determina il modulo del vettore risultante R = o + v e la direzione che il vettore forma con l'asse orizzontale.
Soluzione
Il metodo del parallelogramma viene applicato secondo i passaggi sopra descritti, per ottenere il vettore R. Come detto prima, se i vettori vengono disegnati con cura seguendo la scala e usando il righello e il goniometro, l'ampiezza e la direzione del R vengono misurati direttamente sul disegno.
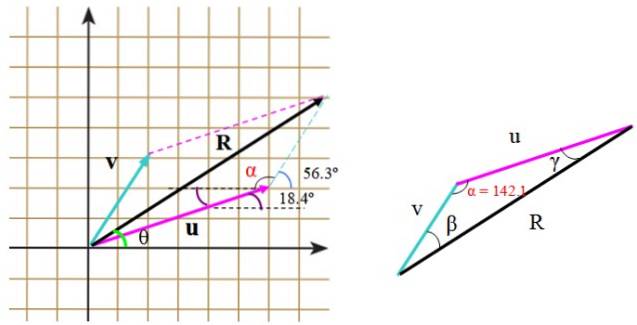
Possono anche essere calcolati direttamente, con l'aiuto della trigonometria e delle proprietà degli angoli. Quando il triangolo formato non è corretto, come in questo caso, viene applicato il teorema del coseno per trovare il lato mancante.
Nel triangolo di destra, i lati misurano u, ve R. Per applicare il teorema del coseno è necessario conoscere l'angolo tra v Y o, che possiamo trovare con l'ausilio della griglia, posizionando opportunamente gli angoli previsti dalla dichiarazione.
Questo angolo è α ed è composto da:
α = (90-56,3º) + 90º + 18,4º = 142,1º
Secondo il teorema del coseno:
RDue = vDue + oDue - 2u⋅v⋅cos α = 3,61Due + 6.32Due - 2 × 3,61 × 6,32 × cos 142,1º = 88,98
R = 9,43 unità.
Infine, l'angolo tra R e l'asse orizzontale è θ = 18,4 º + γ. L'angolo γ può essere trovato usando il teorema del seno:
sin α / R = sin γ / u
Perciò:
sin γ = v (sin α / R) = 3,61 x (sin 142,1º / 9,43)
γ = 13,6º
θ = 18,4º + 13,6º = 32º
- Esercizio 2
Un nuotatore sta per attraversare un fiume nuotando perpendicolarmente alla corrente con una velocità costante di 2.0 m / s. Il nuotatore parte da A, ma finisce in B, un punto a valle, a causa della corrente che lo ha deviato.
Se la velocità della corrente è 0,8 m / se tutte le velocità sono assunte costanti, trova la velocità del nuotatore vista da un osservatore in piedi sulla riva.
Soluzione
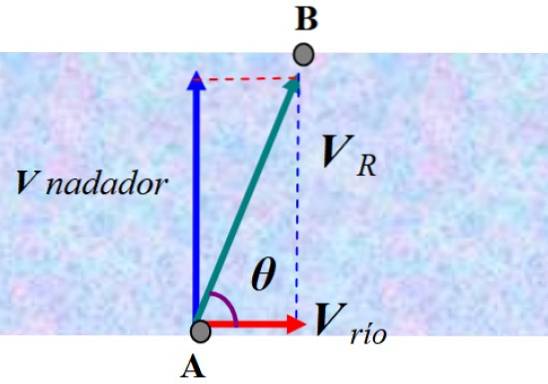
Un osservatore in piedi sulla riva vedrebbe come il nuotatore viene deviato in base alla velocità risultante VR. Per trovare la risposta bisogna sommare vettorialmente la velocità del nuotatore rispetto all'acqua e la velocità della corrente, che chiamiamo V fiume:
V R = V nuotatore + V fiume
Nella figura, che non è in scala, sono stati aggiunti i vettori per ottenere V R. In questo caso, il teorema di Pitagora può essere applicato per ottenere la sua grandezza:
VRDue = 2.0Due + 0.8Due = 4,64
VR = 2,15 m / s
La direzione in cui il nuotatore devia dalla direzione perpendicolare è facilmente calcolabile, notando che:
θ = arctg (2 / 0,8) = 68,2º
Quindi il nuotatore devia di 90º - 68,2º = 27,2º dalla sua direzione originale.
Riferimenti
- Bauer, W. 2011. Fisica per l'ingegneria e le scienze. Volume 1. Mc Graw Hill.
- Bedford, 2000. A. Engineering Mechanics: Statics. Addison Wesley.
- Figueroa, D. (2005). Serie: Fisica per la scienza e l'ingegneria. Volume 1. Cinematica. A cura di Douglas Figueroa (USB).
- Giambattista, A. 2010. Fisica. 2 °. Ed. McGraw Hill.
- Sears, Zemansky. 2016. Fisica universitaria con fisica moderna. 14th. Ed. Volume 1.



Nessun utente ha ancora commentato questo articolo.