
Movimento relativo in una dimensione, in due dimensioni, esercizi
Il moto relativo di una particella o di un oggetto è quello che si osserva rispetto ad un particolare punto di riferimento scelto dall'osservatore, che può essere fisso o in movimento. La velocità si riferisce sempre a un sistema di coordinate usato per descriverla.
Ad esempio, il passeggero di un'auto in movimento e che viaggia comodamente addormentato sul sedile è a riposo rispetto al conducente, ma non per un osservatore in piedi sul marciapiede che vede passare l'auto..

Quindi il movimento è sempre relativo, ma accade che in generale si scelga il sistema di coordinate o di riferimento avendo la sua origine nella Terra o nel suolo, luogo considerato stazionario. In questo modo, l'interesse si concentra sulla descrizione del movimento dell'oggetto in studio..
È possibile descrivere la velocità del copilota addormentato rispetto a un passeggero che viaggia in un'altra macchina? La risposta è si. C'è libertà di scegliere il valore di (xo, Yo, zo): l'origine del sistema di riferimento. La selezione è arbitraria e dipende dalle preferenze dell'osservatore, nonché dalla facilità con cui fornisce la risoluzione del problema..
Indice articolo
- 1 Moto relativo in una dimensione
- 1.1 - Esempio lavorato 1
- 2 Moto relativo in due e tre dimensioni
- 2.1 -Esercizio risolto 2
- 2.2 -Esercizio risolto 3
- 3 Riferimenti
Moto relativo in una dimensione
Quando il movimento avviene lungo una linea retta, i cellulari hanno velocità nella stessa direzione o nella direzione opposta, entrambe viste da un osservatore in piedi sulla Terra (T). L'osservatore si muove rispetto ai cellulari? Sì, con la stessa velocità che portano, ma nella direzione opposta.
Come si muove un cellulare rispetto all'altro? Per scoprirlo, le velocità vengono aggiunte vettorialmente.
-Esempio lavorato 1
Facendo riferimento alla figura mostrata, indicare la velocità relativa della cabina 1 rispetto alla cabina 2 in ogni situazione.
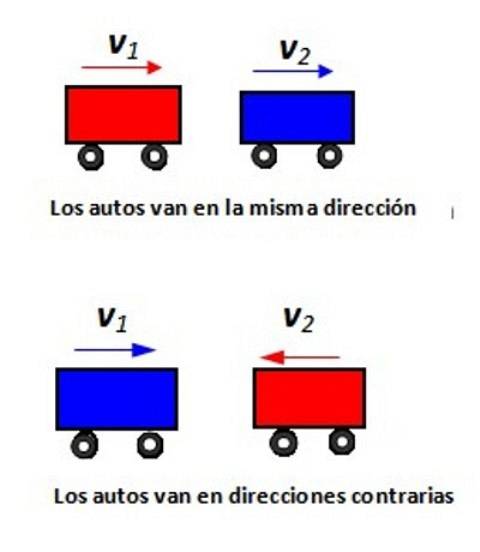
Soluzione
Assegneremo un segno positivo alle velocità a destra e un segno negativo a sinistra. Se un cellulare va a destra a 80 km / h, un passeggero su questo cellulare vede l'osservatore sulla Terra muoversi a - 80 km / h.
Supponiamo che tutto accada lungo l'asse x. Nella figura seguente l'auto rossa si muove a +100 km / h (vista da T) e sta per sorpassare l'auto blu che viaggia a +80 km / h (vista anche da T). Quanto velocemente un passeggero nell'auto blu si avvicina all'auto rossa?
Le etichette sono: v 1/2 velocità dell'auto 1 rispetto all'auto 2, v1 / T velocità della vettura rispetto a T, vT / 2 velocità di T rispetto a 2. Addizione vettoriale:
v1/2 = v1 / T + vT / 2 = (+100 km / h - 80 km / h) X= 20 km / h X
Possiamo fare a meno della notazione vettoriale. Nota i pedici: moltiplicando i due a destra dovresti ottenere quello a sinistra.
E quando vanno dall'altra parte? Ora v1 / T = + 80 km / he v2 / T = -100 km / h, quindi vT / 2 = + 100 km / h. Il passeggero dell'auto blu vedrà avvicinarsi l'auto rossa:
v1/2 = v1 / T + vT / 2 = +80 km / h +100 km / h = 180 km / h
Moto relativo in due e tre dimensioni
Nello schema seguente, r è la posizione dell'aereo vista dal sistema X e Z, r'è la posizione dal sistema X e Z ' Y R è la posizione del sistema con un premio rispetto al sistema senza premio. I tre vettori formano un triangolo in cui R + r'= r, Così r'= r - R.
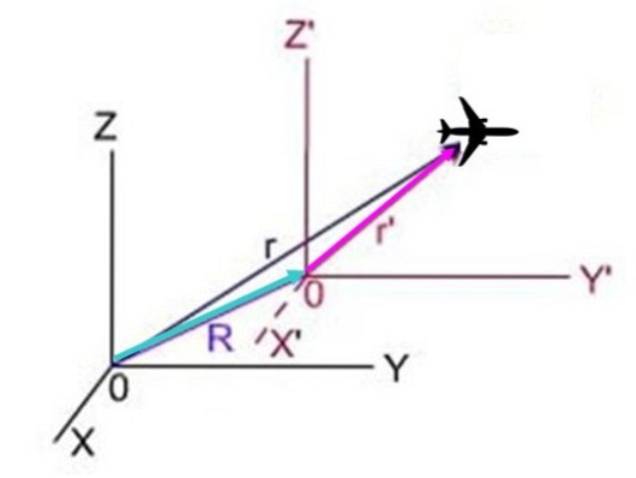
Poiché la derivata rispetto al tempo della posizione è proprio la velocità, risulta:
v'= v - o
In questa equazione v'è la velocità dell'aereo rispetto al sistema X e Z ', v è la velocità rispetto al sistema X e Z Y o è la velocità costante del sistema primo rispetto al sistema non innescato.
-Esercizio risolto 2
Un aereo si sta dirigendo a nord con una velocità di 240 km / h. All'improvviso il vento inizia a soffiare da ovest a est ad una velocità di 120 km / a seconda della terra.
Trova: a) La velocità dell'aereo rispetto al suolo, b) La deviazione sperimentata dal pilota c) La correzione che il pilota deve fare per poter mirare direttamente a nord e la nuova velocità rispetto al suolo, una volta la correzione è stata apportata.
Soluzione
a) Ci sono i seguenti elementi: piano (A), suolo (T) e vento (V).
Nel sistema di coordinate in cui il nord è la direzione + y e la direzione ovest-est è + x, abbiamo le velocità date e la loro rispettiva etichetta (pedici):
v AV = 240 km / h (+Y); v V / T = 120 km / h (+X); v A = ?
La somma vettoriale corretta è:
v A = v AV + v V / T = 240 km / h (+Y) + 120 km / h (+X)
L'entità di questo vettore è: v A = (240 Due+ 120Due)1/2 km / h = 268,3 km / h
b) θ = arctg (v AV / v V / T) = arctg (240/120) = 63,4º Nord Est o 26,6º Nordest.
c) Per continuare a nord con questo vento, dovrai puntare la prua dell'aereo a nord-ovest, in modo che il vento ti spinga direttamente a nord. In questo caso, la velocità dell'aereo visto da terra sarà nella direzione + y, mentre la velocità dell'aereo rispetto al vento sarà nord-ovest (non deve essere necessariamente 26,6º).
Per teorema di Pitagora:
v A = (240 Due- 120Due)1/2 km / h = 207,8 km / h
α = arctg (v V / T / v A ) = arctg (120 / 207,8) = 30º Nordovest
-Esercizio risolto 3
Una persona impiega 2 minuti per scendere una scala mobile fissa. Se la scala funziona, la persona impiega 1 minuto per scendere rimanendo ferma. Quanto tempo impiega la persona a scendere con la scala in esecuzione?
Soluzione
Ci sono tre elementi da considerare: la persona (P), la scala (E) e il terreno (S), le cui velocità relative sono:
vP / E : velocità della persona rispetto alla scala; vÈ: velocità della scala rispetto al suolo; vP / S: velocità della persona rispetto al suolo.
Visto da terra da un osservatore fisso, la persona che scende la scala (E) ha una velocità v P / S dato da:
v P / S = vP / E + vÈ
La direzione positiva sta scendendo la scala. Essere t il tempo necessario per scendere e L distanza. L'entità della velocità della persona v P / S è:
vP / S = L / t
t1 è il tempo necessario per scendere con la scala ferma: v P / E = L / t1
E TDue quello che ti porta giù ancora sulla scala mobile: v È = L / tDue
Combinando le espressioni:
L / t = L / t1 + L / tDue
Sostituzione di valori numerici e risoluzione t:
1 / t = 1 / t1 + 1 / tDue = 1/2 + 1/1 = 1,5
Quindi t = 1 /1,5 minuti = 40 secondi.
Riferimenti
- Bauer, W. 2011. Fisica per l'ingegneria e le scienze. Volume 1. Mc Graw Hill. 84-88.
- Figueroa, D. Physics Series for Sciences and Engineering. Volume 3 °. Edizione. Cinematica. 199-232.
- Giancoli, D. 2006. Fisica: principi con applicazioni. 6th. Ed. Prentice Hall. 62-64.
- Moto relativo. Estratto da: course.lumenlearning.com
- Wilson, J. 2011. Fisica 10. Pearson Education. 166-168.



Nessun utente ha ancora commentato questo articolo.