Il movimento della linea uniforme oppure a velocità costante è quella in cui la particella si muove lungo una linea retta e con velocità costante. In questo modo il cellulare percorre distanze uguali in tempi uguali. Ad esempio, se in 1 secondo percorrerai 2 metri, dopo 2 secondi avrai percorso 4 metri e così via.
Per fare una descrizione accurata del moto, sia esso rettilineo uniforme o altro, è necessario stabilire un punto di riferimento, chiamato anche fonte, rispetto alla quale il mobile cambia posizione.
Se il movimento si svolge interamente lungo una linea retta, è anche importante sapere in quale direzione lo percorre il corpo in movimento.
Su una linea orizzontale, è possibile che il cellulare vada a destra oa sinistra. La distinzione tra le due situazioni è fatta dai segni, la convenzione usuale è la seguente: a destra seguo (+) ea sinistra segno (-).
Quando la velocità è costante, il cellulare non cambia la sua direzione o il suo senso, e anche l'entità della sua velocità rimane invariata..
Indice articolo
Le principali caratteristiche del moto rettilineo uniforme (MRU) sono le seguenti:
-Il movimento scorre sempre lungo una linea retta.
-Un cellulare con MRU percorre distanze o spazi uguali in tempi uguali.
-La velocità rimane invariata sia in grandezza che in direzione e senso.
-MRU manca di accelerazione (nessun cambiamento di velocità).
-Dato che la velocità v rimane costante nel tempo t, il grafico della sua grandezza in funzione del tempo è una linea retta. Nell'esempio in figura 2, la linea è colorata di verde e il valore di velocità viene letto sull'asse verticale, circa +0,68 m / s.
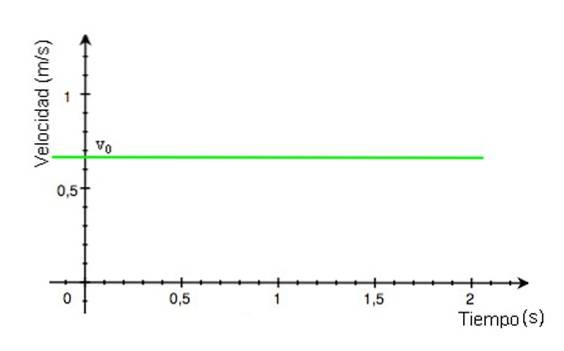
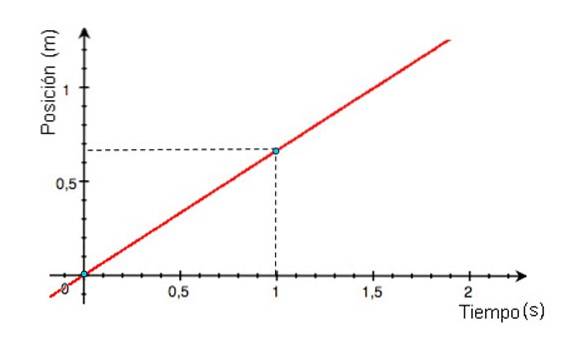
-Il grafico della posizione x rispetto al tempo è una retta, la cui pendenza è uguale alla velocità del mobile. Se la linea del grafico x vs t è orizzontale, il mobile è fermo, se la pendenza è positiva (grafico di figura 3), anche la velocità è positiva.
Conoscere la distanza percorsa dal cellulare quando è disponibile il grafico v vs. è molto semplice. La distanza percorsa è uguale all'area sotto la linea ed entro l'intervallo di tempo desiderato.
Supponiamo di voler conoscere la distanza percorsa dal cellulare di figura 2 nell'intervallo compreso tra 0,5 e 1,5 secondi.
Quest'area è quella del rettangolo ombreggiato in figura 4. Si calcola trovando il risultato della moltiplicazione della base del rettangolo per la sua altezza, i cui valori vengono letti dal grafico.
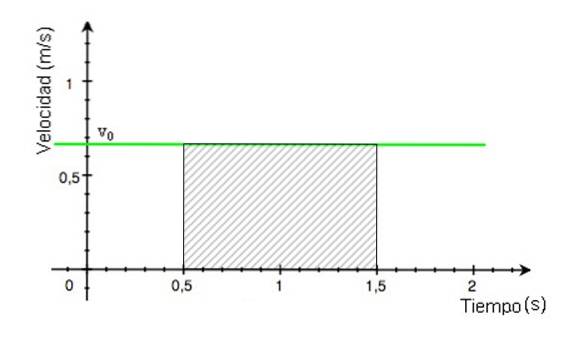
Distanza percorsa = (1,5 - 0,5) x 0,68 m = 0,68 m
La distanza è sempre una quantità positiva, indipendentemente dal fatto che vada a destra oa sinistra..
Nella MRU la velocità media e la velocità istantanea sono sempre le stesse e poiché il loro valore è la pendenza del grafico x vs t corrispondente ad una linea, le equazioni corrispondenti in funzione del tempo sono le seguenti:
-Posizione in funzione del tempo: x (t) = xo + vt
Xo rappresenta la posizione iniziale del mobile, in molte occasioni coincide con l'origine del sistema di riferimento, ma non sempre è così. Questa equazione è anche nota come equazione dell'itinerario.
-Velocità in funzione del tempo: v (t) = costante
Quando v = 0 significa che il cellulare è fermo. Il riposo è un caso particolare di movimento.
-Accelerazione in funzione del tempo: a (t) = 0
Nel moto rettilineo uniforme non ci sono variazioni di velocità, quindi l'accelerazione è zero.
Quando risolvi un esercizio, assicurati che la situazione corrisponda al modello da utilizzare. In particolare, prima di utilizzare le equazioni MRU, è necessario assicurarsi che siano applicabili.
I seguenti esercizi risolti sono problemi con due cellulari.
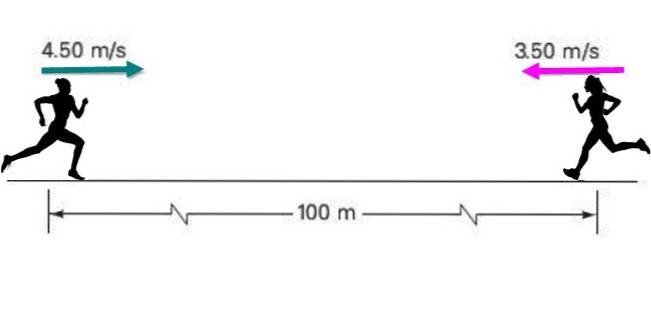
Due atleti si avvicinano tra loro con una velocità costante rispettivamente di 4,50 m / se 3,5 m / s, inizialmente separati da una distanza di 100 metri, come indicato in figura.
Se ognuno mantiene la sua velocità costante, trova: a) Quanto tempo impiegano per incontrarsi? b) Quale sarà la posizione di ciascuno in quel momento?
La prima cosa è indicare l'origine del sistema di coordinate che servirà da riferimento. La scelta dipende dalla preferenza della persona che risolve il problema..
Di solito x = 0 viene scelto proprio nel punto di partenza dei cellulari, può essere nel corridoio sinistro o destro, può anche essere scelto nel mezzo di entrambi.
a) Sceglieremo x = 0 sul corridore sinistro o sul corridore 1, quindi la posizione iniziale di questo è x01 = 0 e per il secondo classificato sarà x02 = 100 m. Il corridore 1 si muove da sinistra a destra con velocità v1 = 4,50 m / mentre il corridore 2 lo fa da destra a sinistra con una velocità di -3,50 m / s.
X1 = x01 + v1t1 = 4,50t1
XDue = x02 + vDuetDue = 100-3,50 tDue
Poiché il tempo è lo stesso per entrambi t1 = tDue = t , quando si incontrano la posizione di entrambi sarà la stessa, quindi X1 = xDue. Abbinamento:
4,50 t = 100-3,50 t
È un'equazione di primo grado per il tempo, la cui soluzione è t = 12,5 s.
b) Entrambi i corridori sono nella stessa posizione, quindi questo sostituisce il tempo ottenuto nella sezione precedente in una qualsiasi delle equazioni di posizione. Ad esempio, possiamo utilizzare quello del broker 1:
X1 = 4,50t1 = 56,25 m
Lo stesso risultato si ottiene sostituendo t = 12,5 s nell'equazione di posizione per il corridore 2.
La lepre sfida la tartaruga a percorrere una distanza di 2,4 km e ad essere onesti gli dà una mezz'ora di vantaggio. Nel gioco, la tartaruga si muove a una velocità di 0,25 m / s, che è il massimo che può correre. Dopo 30 minuti la lepre corre a 2 m / se raggiunge velocemente la tartaruga.
Dopo aver continuato per altri 15 minuti, pensa di avere il tempo di fare un pisolino e vincere comunque la gara, ma si addormenta per 111 minuti. Quando si sveglia corre con tutte le sue forze, ma la tartaruga stava già tagliando il traguardo. Trova:
a) Con quale vantaggio vince la tartaruga?
b) L'istante di tempo in cui la lepre supera la tartaruga
c) Il momento in cui la tartaruga supera la lepre.
La gara inizia tra t = 0. La posizione della tartaruga: XT = 0,25 t
Il movimento della lepre ha le seguenti parti:
-Riposo per il vantaggio che ha dato alla tartaruga: 0 < t < 30 minutos:
-Corri per raggiungere la tartaruga e continua a correre un po 'dopo averla superata; in totale ci sono 15 minuti di movimento.
-Dormi per 111 minuti (riposo)
-Sveglia troppo tardisprint finale)
2,4 km = 2400 m
La durata della gara è stata: t = 2400 m / 0,25 m / s = 9600 s = 160 min. Da questo momento prendiamo 111 minuti dal pisolino e 30 minuti in anticipo, il che significa 19 minuti (1140 secondi). Significa che hai corso per 15 minuti prima di andare a dormire e 4 minuti dopo esserti svegliato per lo sprint.
In questo periodo la lepre coprì la seguente distanza:
dL = 2 m / s. (15. 60 s) + 2 m / s (4. 60 s) = 1800 m + 480 m = 2280 m.
Poiché la distanza totale era di 2400 metri, sottraendo entrambi i valori, risulta che la lepre era a 120 metri dal raggiungimento della meta..
La posizione della lepre prima di addormentarsi è XL = 2 (t - 1800), considerando il ritardo di 30 minuti = 1800 secondi. Corrispondenza xT e xL troviamo il tempo in cui sono:
2 (t - 1800) = 0.25t
2t -0,25 t = 3600
t = 2057,14 s = 34,29 min
Quando la lepre viene superata dalla tartaruga, si è addormentata a 1800 metri dall'inizio:
1800 = 0,25 t
t = 7200 s = 120 min
L'MRU è il movimento più semplice che si possa immaginare ed è per questo che è il primo ad essere studiato in cinematica, ma molti movimenti complessi possono essere descritti come una combinazione di questo e altri semplici movimenti..
Se una persona esce di casa e guida fino a raggiungere una lunga autostrada rettilinea lungo la quale viaggia alla stessa velocità per molto tempo, il suo movimento può essere descritto globalmente come un MRU, senza entrare in maggiori dettagli.
Ovviamente la persona deve fare alcune svolte prima di entrare e uscire dall'autostrada, ma utilizzando questo modello di movimento è possibile stimare la durata del viaggio conoscendo la distanza approssimativa tra il punto di partenza e il punto di arrivo..
In natura, la luce ha un movimento rettilineo uniforme la cui velocità è di 300.000 km / s. Allo stesso modo, si può presumere che il movimento del suono nell'aria sia rettilineo uniforme con una velocità di 340 m / s in molte applicazioni..
Quando si analizzano altri problemi, ad esempio il movimento dei portatori di carica all'interno di un filo conduttore, l'approssimazione MRU può essere utilizzata anche per dare un'idea di cosa accade all'interno del conduttore..
Nessun utente ha ancora commentato questo articolo.