
Movimento pendolare
Qual è il movimento del pendolo?
Il movimento del pendolo È un movimento avanti e indietro compiuto da un oggetto più o meno pesante, chiamato pendolo, sospeso da una corda o da un'asta leggera, fissata all'altra estremità.
Il pendolo riceve un impulso iniziale e viene lasciato oscillare, in questo modo l'oggetto descrive archi avanti e indietro. Questo è il principio di come orologi a pendolo, altalene, sedie a dondolo e metronomi pendolo, utilizzato per segnare i tempi in musica.
Si dice che intorno al 1581, Galileo Galilei osservò l'oscillazione di una lampada nel duomo di Pisa, osservando che, sebbene l'ampiezza dell'oscillazione del candelabro fosse in diminuzione per attrito con l'aria, non la durata del ciclo della lampada..
Questo attirò l'attenzione di Galileo, che decise di proseguire con lo studio e determinò che il periodo del pendolo non dipende dalla massa, ma dalla radice quadrata della lunghezza della corda, come si vedrà in seguito..
Caratteristiche del movimento pendolare
Un pendolo è molto facile da costruire, poiché è sufficiente con un filo a piombo appeso a un filo di cotone e tenuto dall'altra estremità con le dita o fissandolo a un supporto come un chiodo..
Dopo il piccolo impulso iniziale, il peso è incaricato di mantenere in oscillazione il pendolo, sebbene l'attrito diminuisca l'ampiezza del movimento, fino a quando non cessa definitivamente del tutto..
La caratteristica principale del movimento del pendolo è di essere ripetitivo, in quanto è un movimento avanti e indietro. Ora, per facilitarne lo studio, è conveniente fare alcune semplificazioni per concentrarsi su un modello più semplice, chiamato il pendolo semplice.
Il semplice pendolo

È un sistema ideale che consiste in un filo a piombo, considerato come una massa puntiforme m, attaccato a una corda leggera e inestensibile di lunghezza L. Le caratteristiche di questo sistema sono:
- Avere un movimento ripetitivo e periodico, consistente nell'andare avanti e indietro per un arco di circonferenza di raggio pari a L..
- Non tiene conto dell'attrito.
- La gamma di movimento è piccola (< 5º).
- Il periodo è indipendente dalla massa m, e dipende esclusivamente dalla lunghezza L pendolo.
Formule ed equazioni
Quello che segue è un diagramma del pendolo semplice, sul quale agiscono due forze: il peso P di magnitudo mg, che è diretto verticalmente verso il basso e la tensione T Sulla corda. L'attrito non viene considerato.
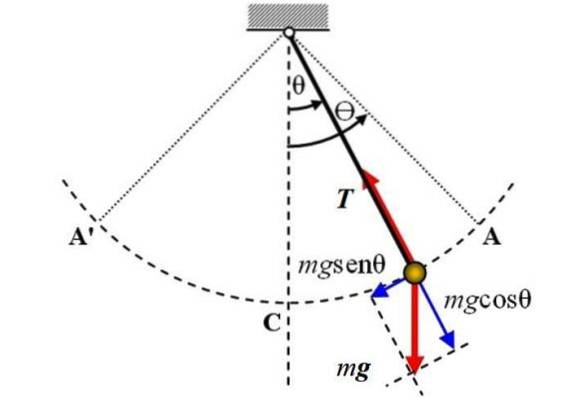
L'asse di riferimento è l'asse verticale e coincide con la posizione θ = 0, da lì si misura lo spostamento angolare θ, in una direzione o nell'altra. Il segno + può essere assegnato allo spostamento a destra nella figura.
Per studiare il movimento del pendolo, viene scelto un sistema di coordinate con l'origine del pendolo stesso. Questo sistema ha una coordinata tangenziale all'arco di circonferenza A'CA descritto dal pendolo, nonché una coordinata radiale, diretta verso il centro della traiettoria..
Nell'istante mostrato in figura, il pendolo si muove verso destra, ma la componente tangenziale della gravità, chiamata Ft, è responsabile di farlo tornare. Si può vedere dalla figura che questo componente ha la direzione opposta al movimento.
Per quanto riguarda la tensione nella corda, è bilanciata con la componente del peso mgcosθ.

Spostamento angolare
Dobbiamo esprimere l'equazione in termini di una singola variabile, ricordando che lo spostamento angolare θ e l'arco percorso sono legati dall'equazione:
s = L.θ
La massa si annulla su entrambi i lati e se l'ampiezza è piccola anche l'angolo,, per cui vale la seguente approssimazione:
sen θ ≈ θ
Con ciò si ottiene la seguente equazione differenziale per la variabile θ (t):


Questa equazione è molto facile da risolvere, poiché la sua soluzione è una funzione la cui derivata seconda è la funzione stessa. Esistono tre alternative: un coseno, un seno o un esponenziale. La funzione coseno è scelta per lo spostamento angolare θ (t), poiché è una funzione ben nota e facile da gestire.
Il lettore può verificare, differenziando due volte, che la seguente funzione soddisfa l'equazione differenziale:
θ (t) = θm cos (ωt + φ)
Dove θm è l'angolo massimo che il pendolo muove rispetto alla verticale e la frequenza angolare ω è:

Equazione del periodo
Il periodo T del movimento è il tempo necessario per eseguire un ciclo ed è definito come:

Sostituendo ω:

Come detto sopra, il periodo non dipende dalla massa del pendolo, ma solo dalla sua lunghezza..
Esempi di movimento del pendolo
Misurazione della frequenza cardiaca
Galileo ha avuto l'idea di misurare la frequenza cardiaca delle persone, regolando la lunghezza del pendolo per far coincidere il periodo con i battiti del cuore di una persona.
L'orologio a pendolo
Questo è senza dubbio uno degli esempi più familiari di movimento del pendolo. La produzione di orologi a pendolo riguarda tanto la scienza quanto l'arte. Il fisico olandese Christian Huygens (1629-1695) sviluppò il primo orologio a pendolo nel 1656, basandosi sullo studio fatto anni fa da Galileo.
Il pendolo di Foucault

È un pendolo un po 'diverso da quello descritto sopra, poiché è in grado di ruotare su qualsiasi piano verticale. È stato creato dal fisico francese Léon Foucault (1819-1868) e viene utilizzato per visualizzare la rotazione della Terra.
Esercizio risolto
Un semplice pendolo passa ogni 0,5 s attraverso la posizione di equilibrio. Qual è la lunghezza del filo?
Soluzione
Poiché il periodo è il tempo necessario per completare un ciclo completo, in cui si attraversa due volte la posizione di equilibrio: l'una che va e l'altra che torna, quindi:
T = 2 × 0,5 s = 1 s
A partire dal:

La lunghezza L del filo viene cancellata:

Il filo è lungo 0,25 mo 25 cm.
Riferimenti
- Figueroa, D. (2005). Serie: Fisica per la scienza e l'ingegneria. Volume 2. Dinamica. A cura di Douglas Figueroa (USB).
- Giambattista, A. 2010. Fisica. 2 °. Ed. McGraw Hill.
- Giancoli, D. 2006. Fisica: principi con applicazioni. 6 °. Ed prentice hall.
- Katz, D. 2013. Fisica per scienziati e ingegneri. Fondamenti e connessioni. Cengage Learning.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.



Nessun utente ha ancora commentato questo articolo.