
Formule, esempi, applicazioni, esercizi della legge di Hooke
Il Legge di Hooke sottolinea che la deformazione subita da un oggetto elastico è direttamente proporzionale alla forza ad esso applicata. La costante di proporzionalità dipende dalla natura dell'oggetto, dalla sua geometria e dal materiale con cui è realizzato..
Tutti i materiali hanno proprietà elastiche in misura maggiore o minore, quindi sono conformi alla legge di Hooke fintanto che tornano alle loro dimensioni originali, una volta cessata la forza. Le molle e gli elastici sono buoni esempi di oggetti che soddisfano la legge di Hooke, ma lo sono anche i perni d'acciaio che fanno parte di un ponte.

Prendendo una molla o una molla come esempio, per mantenerla tesa o compressa, è necessario applicare una forza di magnitudo F. Secondo la legge di Hooke, la molla subirà una deformazione x:
F ∝ x
La costante della proporzionalità, che essendo una molla si chiama costante di rigidità della molla, è indicato come k, quindi:
F = k⋅x
Nelle unità del Sistema Internazionale, la forza è in newton (N) e la deformazione in metri (m). Pertanto, la costante della molla ha unità di N / m. La costante della molla rappresenta la forza che deve essere applicata per deformarla di 1 m di lunghezza.
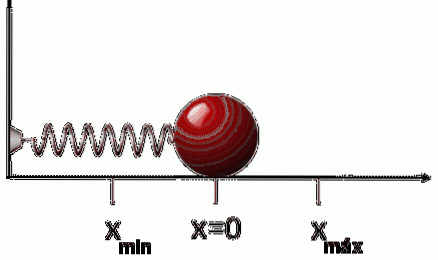
Se, dopo aver teso o compresso la molla, viene rilasciata, si muoverà nella direzione opposta alla forza applicata. Ciò significa che se lo allunghiamo, si comprime e viceversa. Da qui la forza FR che cosa la primavera esercita è:
FR = -k⋅x
Il segno negativo indica quanto sopra: che la forza si oppone allo spostamento, quindi questa forza è nota come forza riparatrice.
Indice articolo
- 1 Formula ed equazioni
- 1.1 Lavoro svolto per allungare o comprimere una molla
- 2 Esempi di molle
- 2.1 Molla di compressione
- 2.2 Molle di estensione e torsione
- 2.3 Materiali per la fabbricazione delle molle
- 3 Applicazioni della legge di Hooke
- 4 Esercizi risolti
- 4.1 - Esercizio 1
- 4.2 - Esercizio 2
- 5 Riferimenti
Formula ed equazioni
La relazione tra forza e spostamento in una molla è stata scoperta da Robert Hooke (1635-1703), un notevole fisico inglese noto per la sua rivalità con Isaac Newton. Hooke era uno scienziato versatile che si è avventurato con successo in diversi campi della scienza: meccanica, biologia, astronomia e architettura..

Hooke si rese conto che se la forza applicata a una molla non è molto grande, la molla si deforma proporzionalmente alla forza, e una volta che quella forza scompare, la molla ritorna alla sua lunghezza naturale.
Pertanto, la legge di Hooke in forma grafica ha la forma di una linea retta, la cui pendenza è la costante della molla. L'immagine seguente mostra la forza esercitata sulla molla per allungarla - o comprimerla - in funzione della posizione x. Notare inoltre che la forza non dipende dalla lunghezza naturale della molla, ma dal suo spostamento..
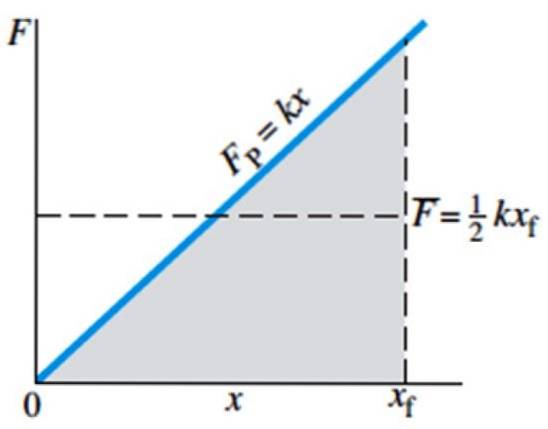
La forza media è indicata nel grafico dalla barra F ed è pari a ½ kxF, dove xF è la posizione finale della molla.
Sia la forza esercitata sulla molla, sia la forza che esercita su un oggetto ad essa legato, sono forze variabili. Più si desidera allungare o comprimere la molla, maggiore sarà la forza da applicare per ottenerla..
Lavoro svolto per allungare o comprimere una molla
Quando una forza di deformazione viene applicata alla molla, viene eseguito il lavoro che viene immagazzinato nella molla e può essere utilizzato in seguito..
Il lavoro meccanico è definito come l'area sotto il grafico della forza F in funzione della posizione x. Per calcolare il lavoro W che una forza variabile F (x) fa quando sposta un oggetto dalla posizione x1 fino alla posizione xDue dobbiamo calcolare l'integrale definito:
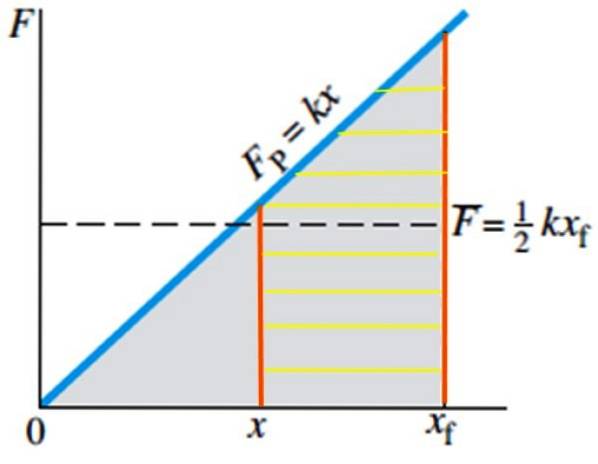
Nel caso del lavoro necessario per portare una molla dalla sua posizione di equilibrio alla posizione xF È molto semplice, poiché l'area da calcolare è quella del triangolo ombreggiato in grigio in figura 4, la cui formula è nota:
Area del triangolo = ½ base. altezza
Pertanto il lavoro necessario è:
W = ½ xF . (kxF) = ½ k (xF)Due
E se vuoi calcolare il lavoro necessario per portare la molla dalla posizione x alla posizione xF, sarebbe equivalente al calcolo dell'area del trapezio tratteggiato nella figura 5:
W = ½ k (xF)Due - ½ k xDue

Esempi di molle
A seconda dell'applicazione a cui sono destinate, le molle possono essere elicoidali, cilindriche, coniche, a spirale, a sezione circolare (le più comuni), quadrate o rettangolari..
Una classificazione molto utilizzata è in base al tipo di sforzo a cui verranno sottoposte: sono presenti le molle di torsione, flessione, compressione ed estensione. Questi ultimi sono ampiamente utilizzati e alcuni funzionano allo stesso modo per la tensione e la compressione..
Molla di compressione
Un esempio di una molla di compressione è quella utilizzata nel giocattolo chiamato pogo o bastone da salto. Queste molle immagazzinano molta energia potenziale quando vengono compresse e la rilasciano a poco a poco quando tornano alla posizione di equilibrio. In questo modo i rimbalzi non sono troppo bruschi.

Molle di estensione e torsione
Le molle del trampolino sono del tipo a molla di estensione e sono prodotte con bobine strettamente avvolte, con due ganci alle estremità. Sono in grado di trattenere molta energia potenziale, che poi rilasciano quando qualcuno si arrampica e inizia a saltare sul tappeto, che ha anche una sua risposta elastica, come tutti i materiali..
Le molle a torsione sono molto comuni, perché vengono utilizzate per realizzare mollette. Invece di ganci alle estremità, si piegano ad angolo per resistere alle forze di torsione.

Materiali per la produzione di molle
I materiali più adatti per la realizzazione delle molle sono quelli con a ultima resistenza (resistenza finale) alta, cioè supportano un grande sforzo prima di rompersi. È anche auspicabile che il materiale abbia un alto punto di snervamento, in modo che non perda le sue qualità elastiche con piccoli sforzi..
Le molle per carichi pesanti sono realizzate in leghe tra cui acciaio ad alto tenore di carbonio, rame, nichel e bronzo.
Applicazioni della legge di Hooke
Poiché le molle hanno la virtù di immagazzinare energia potenziale quando vengono allungate o compresse, sono in grado di funzionare muovendo cose come meccanismi..
In questo modo le molle hanno una moltitudine di applicazioni, dai piccoli oggetti di uso quotidiano, passando per le automobili, ai macchinari di ogni tipo. Le molle servono per:
-Attenua le vibrazioni.
-Meccanismi retrattili di fabbricazione: penne, mollette, fermagli per capelli.
-Realizza bilance a molla o dinamometri
E fanno anche parte del meccanismo di:
-Orologi.
-Trampolini.
-Serrature.
-Giocattoli.
-Armi.
-I misuratori ad ago, ad esempio il galvanometro, utilizzati per misurare correnti, tensioni e resistenze.
Esercizi risolti
- Esercizio 1
Una forza di magnitudine 5,0 N viene applicata a una molla, provocando l'allungamento di una lunghezza di 3,5 cm dalla sua lunghezza naturale..
a) Quanto si allunga quando la forza applicata è 7 N?
b) Trovare il lavoro svolto dalla forza applicata per allungare la molla di 3,5 cm dalla sua lunghezza naturale.
Soluzione a
Sapendo che la molla viene allungata di 3,5 cm applicando 5,0 N possiamo calcolarne la costante:
k = F / x = 5,0 N / 3,5 cm = 1,43 N / cm.
Quando viene applicata una forza di 7 N, si ottiene il seguente allungamento:
x = F / k = 7,0 N / 1,43 N / m = 4,9 cm
Soluzione b
Il lavoro necessario per deformare una molla è dato da:
W = ½ kxDue = 0,5 x 1,43 N / cm x (3,5 cm)Due = 8,76 N. cm = 8,76 N. 1 x10 -Due m = 0,0876 J.
- Esercizio 2
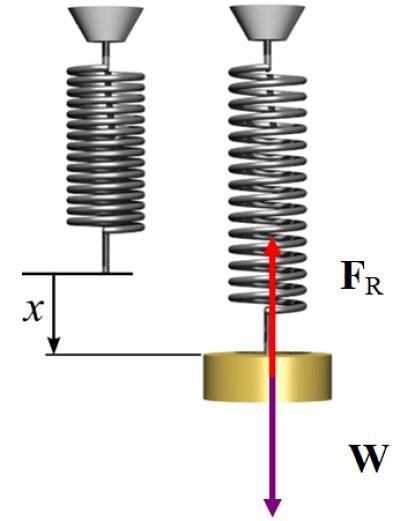
Una molla di massa trascurabile e lunga 10 cm è sospesa a un supporto. Se vi è appesa una massa di 2 kg, la molla viene allungata a 15 cm. Calcolare:
a) La costante della molla
b) La dimensione della molla quando è sospesa una massa di 3 kg.
Soluzione a
Il tratto primaverile è x = 15-10 cm = 5 cm
Essendo il sistema in equilibrio statico, la forza esercitata dalla molla in fase di allungamento è diretta verticalmente verso l'alto, per compensare il peso, che è diretto verso il basso, quindi:
FR = W → kx = mg
k = 2 x 9,8 N / 5 x10 -Due m = 392 N / m
Soluzione b
Quando viene sospeso un peso di 3 kg, la nuova forza è W = 3 x 9,8 N = 29,4 N
In tal caso il tratto è:
x = mg / k = 29. 4 N / 392 N / m = 0,075 m = 7,5 cm
Riferimenti
- Bauer, W. 2011. Fisica per l'ingegneria e le scienze. Volume 1. Mc Graw Hill.
- Blog sui meccanismi creativi. Quattro diversi tipi di molle. Estratto da: creativemechanisms.com.
- Figueroa, D. (2005). Serie: Fisica per la scienza e l'ingegneria. Volume 2. Dinamica. A cura di Douglas Figueroa (USB).
- Giancoli, D. 2006. Fisica: principi con applicazioni. 6 °. Ed. Prentice Hall.
- .



Nessun utente ha ancora commentato questo articolo.