
Ne risulta forza il modo in cui viene calcolato e gli esercizi risolti
Il vigore risultante è la somma di tutte le forze che agiscono sullo stesso corpo. Quando un corpo o un oggetto è soggetto all'azione di più forze contemporaneamente, si verifica un effetto. Le forze di azionamento possono essere sostituite da una singola forza che produce lo stesso effetto. Questa forza singola è la forza risultante nota anche come forza netta ed è rappresentata dal simbolo FR .
L'effetto che produce FR dipenderà dalle sue dimensioni, direzione e senso. Le quantità fisiche che hanno direzione e senso sono quantità vettoriali.
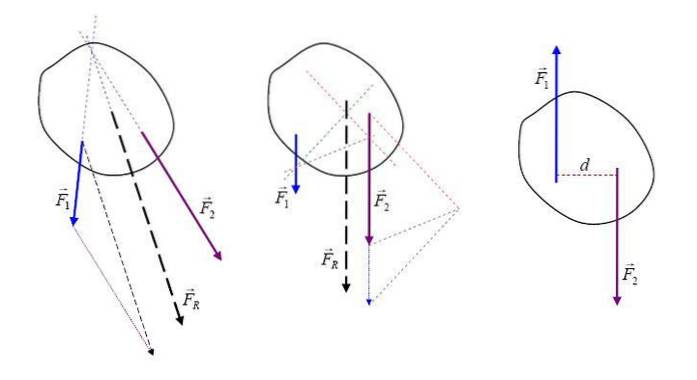
Essendo le forze che agiscono sulle grandezze di un vettore del corpo, la forza risultante FR è una somma vettoriale di tutte le forze e può essere rappresentata graficamente con una freccia che ne indica la direzione e la direzione.
Con la forza risultante si semplifica il problema di un corpo soggetto a più forze riducendolo ad una sola forza agente.
Indice articolo
- 1 Formula
- 2 Come si calcola la forza risultante?
- 2.1 risultante di forze parallele
- 2.2 Forze non parallele
- 3 esercizi risolti
- 4 Riferimenti
Formula
La rappresentazione matematica della forza risultante è una somma vettoriale delle forze.
FR= ∑F (1)
∑F = F1+ FDue+ F3+... FN (Due)
FR= Forza risultante
∑F = Somma delle forze
N= Numero di forze
La forza risultante può anche essere rappresentata dall'equazione della seconda legge di Newton.
FR= m.per (3)
m= massa corporea
a = accelerazione del corpo
Se l'equazione (1) viene sostituita nell'equazione (3), si ottengono le seguenti equazioni:
∑F = m.per (4)
F1+ FDue+ F3+... FN = m.per (5)
Le espressioni matematiche (4) e (5) forniscono informazioni sullo stato del corpo ottenendo il vettore di accelerazione per.
Come si calcola la forza risultante?
La forza risultante si ottiene applicando la seconda legge di Newton che afferma quanto segue:
La forza netta che agisce su un corpo è uguale al prodotto della sua massa e dell'accelerazione che acquisisce. (Equazione (3))
L'accelerazione del corpo avrà la direzione della forza netta applicata. Se tutte le forze che agiscono sul corpo sono note, basterebbe sommarle vettorialmente per ottenere la forza risultante. Allo stesso modo, se la forza risultante è nota, sarebbe sufficiente dividerla per la massa del corpo per ottenere la sua accelerazione.
Se la forza risultante è zero, il corpo è a riposo oa velocità costante. Se una singola forza agisce sul corpo, la forza risultante è uguale a quella forza FR=F.
Quando più forze agiscono sullo stesso corpo, è necessario prendere in considerazione le componenti vettoriali della forza e se queste forze sono parallele o meno.
Ad esempio, se facciamo scorrere orizzontalmente un libro posto su un tavolo, le forze in direzione orizzontale sono le uniche che forniscono accelerazione al corpo. La forza verticale netta sul libro è zero.
Se la forza applicata al libro ha un'inclinazione rispetto al piano orizzontale del tavolo, la forza viene scritta in funzione delle componenti verticale e orizzontale.
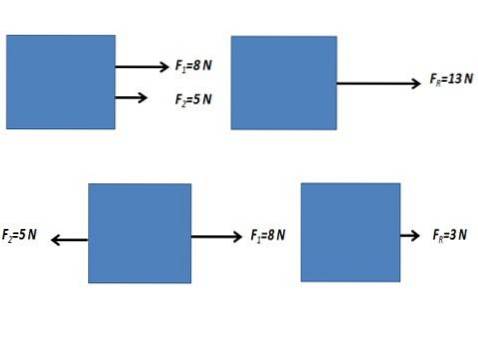
Risultante forze parallele
Le forze parallele che agiscono su un corpo sono quelle forze che agiscono nella stessa direzione. Possono essere di due tipi di senso uguale o opposto.
Quando le forze agenti su un corpo hanno la stessa direzione e la stessa direzione o sono nella direzione opposta, la forza risultante si ottiene eseguendo la somma algebrica dei valori numerici delle forze.
Forze non parallele
Quando forze non parallele vengono applicate a un corpo, la risultante delle forze avrà componenti rettangolari e verticali. L'espressione matematica per calcolare la forza netta è:
FRDue= (∑ FX)Due+(∑ FY)Due (6)
così θX= ∑ FY / ∑ FX (7)
∑ FX e ∑ FX= Somma algebrica delle componenti X e Y delle forze applicate
θX= angolo formato dalla forza risultante FR con albero X
Si noti che la forza di espressione risultante (6) non è evidenziata in grassetto ed è perché esprime solo il valore numerico. La direzione è determinata dall'angolo θX.
L'espressione (6) è valida per forze che agiscono sullo stesso piano. Quando le forze agiscono nello spazio, il componente viene preso in considerazione z di forza quando si lavora con componenti rettangolari.
Esercizi risolti
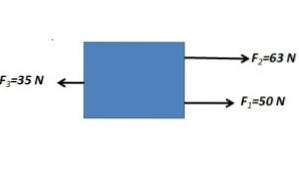
Le forze parallele nella stessa direzione vengono sommate e sottratte con la forza parallela nella direzione opposta
FR= 63 N + 50 N - 35 N = 78N
La forza risultante ha una grandezza di 78N con direzione orizzontale.
2. Calcola la forza risultante di un corpo sotto l'influenza di due forze F1 Y FDue. La forza F1 ha una magnitudine di 70N e viene applicato orizzontalmente. La forza FDue ha una magnitudine di 40 N e viene applicato con un angolo di 30 ° rispetto al piano orizzontale.
Per risolvere questo esercizio, viene disegnato un diagramma a corpo libero con gli assi delle coordinate X e Y
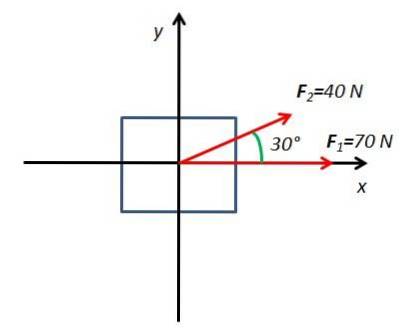
Tutti i componenti sono determinati X e Y delle forze che agiscono sul corpo. La forza F1 ha solo una componente orizzontale sull'asse X. La forza FDue ha due componenti F2x e F2 e che si ottengono dalle funzioni seno e coseno dell'angolo 30 °.
F1x = F1=70N
F2x = FDue cos 30 ° = 40 N.cos 30 ° = 34,64N
F1y = 0
F2 e= FDue senza 30 ° = 40 senza 30 ° = 20N
∑ FX =70 N + 34,64 N = 104,64 N.
∑ FY=20N + 0 = 20N
Una volta determinate le forze risultanti nell'albero X e Y procediamo per ottenere il valore numerico della forza risultante.
FRDue= (∑ FX)Due+(∑ FY)Due
La forza risultante è la radice quadrata della somma delle componenti al quadrato delle forze
FR= √ (104.64N)Due+(20N)Due
FR= 106.53N
L'angolo formato dalla forza risultante FR si ottiene dalla seguente espressione:
θX= così-1(∑ FY / ∑ FX)
θX= così-1(20N / 104,64 N) = 10,82 °
La forza risultante FR ha una magnitudine di 106,53N e ha una direzione determinata dall'angolo di 10,82 ° che forma con l'orizzontale.
Riferimenti
- Dola, G, Duffy, M e Percival, A. Fisica. Spagna: Heinemann, 2003.
- Avison, J H. Il mondo della fisica. India: Thomas Nelson and Sons, 1989.
- Pinsent, M. Processi fisici. Regno Unito: Nelson Thomas, 2002.
- Yadav, S K. Meccanica di ingegneria. Delhi: Discovery Publishing House, 2006.
- Serway, RA e Jewett, J W.. Fisica per scienziati e ingegneri. California, USA: Brooks / Cole, 2010.


Nessun utente ha ancora commentato questo articolo.