
Forza di taglio superficiale e forze di massa
Il forza di taglio È una forza composta che si caratterizza per essere parallela alla superficie su cui viene esercitata e tende a dividere il corpo spostando le sezioni risultanti dal taglio..
È schematicamente rappresentato nella figura 1, in cui è mostrata una forza di taglio applicata a due diversi punti di una matita di legno. La forza di taglio a sua volta richiede due forze parallele e opposte, che a seconda della loro intensità, sono in grado di deformare la matita o di fratturarla definitivamente..
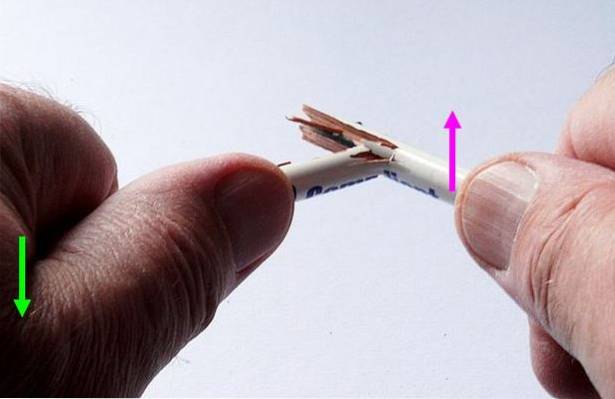
Quindi, anche se parliamo di forza di taglio al singolare, in realtà si applicano Due forze, poiché la forza di taglio è a forza composta. Queste forze sono costituite da due forze (o più, in casi complessi) applicate in punti diversi su un oggetto.
Due forze della stessa grandezza e direzione opposta, ma con linee di azione parallele, costituiscono a coppia. Le coppie non forniscono la traslazione agli oggetti, poiché la loro risultante è zero, ma forniscono una coppia netta.
Con una coppia, oggetti come il volante di un veicolo vengono ruotati, oppure possono essere deformati e rotti, come nel caso della matita e della tavola di legno mostrata in figura 2.
Indice articolo
- 1 Forze superficiali e forze di massa
- 1.1 Forze semplici e forze composte
- 2 Sforzo di taglio
- 2.1 Stress e tensione
- 2.2 Il modulo di taglio
- 3 Riferimenti
Forze di superficie e forze di massa
Le forze composte fanno parte del cosiddetto forze superficiali, proprio perché sono applicati alla superficie dei corpi e non sono in alcun modo legati alla loro massa. Per chiarire il punto, confrontiamo queste due forze che agiscono frequentemente sugli oggetti: peso e forza di attrito..
L'entità del peso è P = mg e poiché dipende dalla massa del corpo, non è una forza superficiale. È un forza di massa, e il peso è l'esempio più caratteristico.
Tuttavia, l'attrito dipende dalla natura delle superfici di contatto e non dalla massa del corpo su cui agisce, quindi è un buon esempio di forze superficiali che compaiono frequentemente..
Forze semplici e forze composte
Le forze di superficie possono essere semplice o composto. Abbiamo già visto un esempio di forza composta nella forza di taglio, e da parte sua l'attrito è rappresentato come una forza semplice, poiché è sufficiente una singola freccia per rappresentarla nel diagramma del corpo isolato dell'oggetto..
Le forze semplici sono responsabili della stampa delle modifiche al movimento di un corpo, ad esempio sappiamo che la forza di attrito cinetico tra un oggetto in movimento e la superficie su cui si muove, si traduce in una riduzione della velocità.
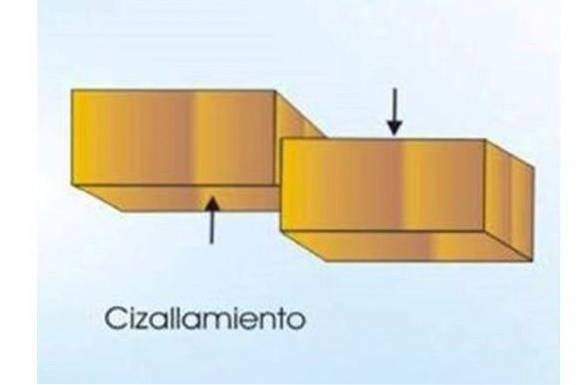
Al contrario, le forze composte tendono a deformare i corpi e nel caso di cesoie o cesoie il risultato finale può essere un taglio. Altre forze superficiali come la tensione o la compressione allungano o comprimono il corpo su cui agiscono.
Ogni volta che si taglia il pomodoro per preparare la salsa o si usa una forbice per tagliare un foglio di carta, valgono i principi descritti. Gli utensili da taglio di solito hanno due lame di metallo affilate per applicare la forza di taglio sulla sezione trasversale dell'oggetto da tagliare..

Sforzo di taglio
Gli effetti della forza di taglio dipendono dall'entità della forza e dall'area su cui agisce, quindi nell'ingegnerizzare il concetto di sforzo di taglio, che tiene conto sia della forza che dell'area.
Questo sforzo ha altri significati come resistenza al taglio o shear stress e nelle costruzioni civili è estremamente importante considerarlo, poiché molti cedimenti nelle strutture derivano dall'azione delle forze di taglio.
La sua utilità si capisce subito se si considera la seguente situazione: supponiamo di avere due barre dello stesso materiale ma di diverso spessore che vengono sottoposte a forze crescenti fino alla rottura..
È evidente che per rompere la barra più spessa occorre applicare una forza maggiore, tuttavia lo sforzo è lo stesso per qualsiasi barra che abbia la stessa composizione. Test come questo sono frequenti in ingegneria, data l'importanza di selezionare il materiale giusto affinché la struttura progettata funzioni in modo ottimale..
Stress e tensione
Matematicamente, se lo sforzo di taglio è indicato come τ, Alla grandezza della forza applicata come F e all'area su cui agisce come A, abbiamo lo sforzo di taglio medio:
τmedia= F / A
Essendo il rapporto tra forza e area, l'unità di sforzo nel Sistema Internazionale è il newton / mDue, chiamato Pascal e abbreviato in Pa. Nel sistema inglese si usa la libbra-forza / piede Due e la libbra-forza / polliceDue.
Tuttavia, in molti casi l'oggetto sottoposto alla sollecitazione di taglio si deforma e quindi riprende la sua forma originaria senza effettivamente rompersi, una volta che la sollecitazione ha cessato di agire. Supponiamo che la deformazione consista in un cambiamento di lunghezza.
In questo caso lo stress e la deformazione sono proporzionali, quindi si può considerare quanto segue:
Resistenza al taglio ∝ Deformazione dell'unità
Il simbolo ∝ significa “proporzionale a” e per quanto riguarda la deformazione unitaria, è definito come il quoziente tra la variazione di lunghezza, che si chiamerà ΔL e la lunghezza originaria, denominata Lo. In questo modo:
τ ∝ (ΔL / Lo)
Modulo di taglio
Essendo un quoziente tra due lunghezze, la deformazione non ha unità, ma quando si posiziona il simbolo di uguaglianza, la costante di proporzionalità deve fornirle. Chiamando G a detta costante:
τ = G (ΔL / Lo)
Si chiama G. modulo di taglio o modulo di taglio. Ha unità Pascal nel Sistema Internazionale e il suo valore dipende dalla natura del materiale. Tali valori possono essere determinati in laboratorio testando l'azione di forze diverse su campioni di varia composizione..
Quando è necessario determinare l'entità della forza di taglio dall'equazione precedente, è sufficiente sostituire la definizione di sollecitazione:
τ = F / A = G (ΔL / Lo)
E chiaro:
F = A × G (ΔL / Lo)
Le forze di taglio sono molto frequenti e i loro effetti devono essere presi in considerazione in molti aspetti della scienza e della tecnologia. Nelle costruzioni compaiono nei punti di appoggio delle travi, possono insorgere durante un incidente e rompersi un osso e la loro presenza è in grado di alterare il funzionamento dei macchinari..
Agiscono su larga scala sulla crosta terrestre, provocando fratture rocciose e incidenti geologici, grazie all'attività tettonica. Pertanto sono anche responsabili della formazione continua del pianeta.
Riferimenti
- Beer, F. 2010. Meccanica dei materiali. 5 °. Edizione. McGraw Hill. 7 - 9.
- Fitzgerald, 1996. Meccanica dei materiali. Alfa Omega. 21-23.
- Giancoli, D. 2006. Fisica: principi con applicazioni. 6tth Ed. Prentice Hall. 238-242.
- Hibbeler, R.C. 2006. Meccanica dei materiali. 6 °. Edizione. Pearson Education. 22-25
- Valera Negrete, J. 2005. Note sulla fisica generale. UNAM. 87-98.
- Wikipedia. Shear Stress. Estratto da: en.wikipedia.org.



Nessun utente ha ancora commentato questo articolo.