
Sforzo normale in cosa consiste, come viene calcolato, esempi
Il sforzo normale applicata ad un certo materiale, detta anche sollecitazione uniassiale, è la relazione che esiste tra la forza applicata perpendicolarmente su una certa superficie e l'area della sezione trasversale su cui agisce, ovvero il carico per unità di superficie. Matematicamente, se P è l'ampiezza della forza e A è l'area in cui viene applicata, la sollecitazione σ è il quoziente: σ = P / A.
Le unità di sollecitazione normale nel Sistema Internazionale sono newton / metroDue, noto come Pascal e abbreviato Pa. Queste sono le stesse unità di pressione. Altre unità che appaiono frequentemente in letteratura sono libbre / pollice.Due o psi.

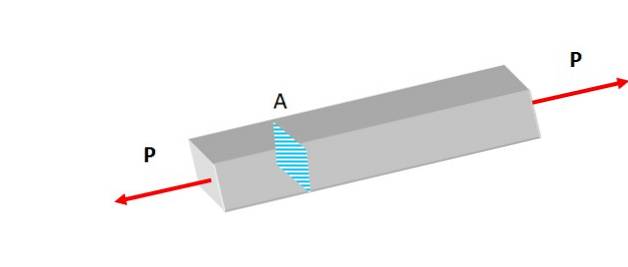
Nella figura 2 due forze di uguale grandezza vengono applicate perpendicolarmente all'area della sezione trasversale, esercitando una leggerissima trazione sulla barra che tende ad allungarla..
Queste forze producono uno stress normale che viene anche chiamato carico assiale centrato, perché la sua linea di azione coincide con l'asse assiale, su cui giace il baricentro.
Gli sforzi, normali o meno, compaiono continuamente in natura. Nella litosfera, le rocce sono soggette a gravità e attività tettonica, subendo deformazioni.
Nascono così strutture come pieghe e faglie, il cui studio è importante nello sfruttamento dei minerali e nell'ingegneria civile, per la costruzione di edifici e strade, solo per citare alcuni esempi..
Indice articolo
- 1 Come viene calcolato?
- 2 Legge di Hooke e stress normale
- 3 Importanza dello stress nella resistenza dei materiali e geologia
- 4 esempi
- 4.1 -Esercizio 1
- 4.2 -Esercizio 2
- 5 Riferimenti
Come viene calcolato?
L'equazione data all'inizio σ = P / A permette di calcolare la sollecitazione normale media sull'area in questione. Il valore di P è l'ampiezza della forza risultante sull'area applicata al baricentro ed è sufficiente per molte semplici situazioni.
In questo caso, la distribuzione delle forze è uniforme, soprattutto nei punti lontani da dove la barra è soggetta a tensione o compressione. Ma se è necessario calcolare lo stress in un punto specifico o le forze non sono distribuite uniformemente, è necessario utilizzare la seguente definizione:
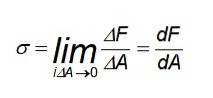
Quindi, in generale, il valore della sollecitazione in un punto particolare può essere diverso dal valore medio. Lo sforzo, infatti, può variare a seconda della sezione da considerare..
Ciò è illustrato nella figura seguente, in cui le forze di trazione F cercano di separare la barra di equilibrio nelle sezioni mm Y nn.
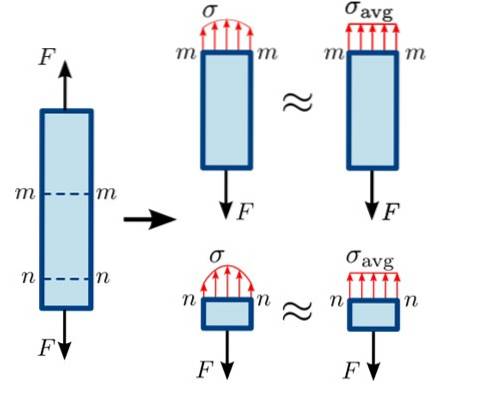
Come sezione nn è molto vicino a dove viene applicata la forza F verso il basso, la distribuzione delle forze sulla superficie non è completamente omogenea, minore è la forza più ci si allontana da quel punto. La distribuzione è un po 'più omogenea nella sezione mm.
In ogni caso, lo sforzo normale tende sempre ad allungare o comprimere le due parti del corpo che si trovano su entrambi i lati del piano su cui agiscono. D'altra parte, altri sforzi diversi, come il taglio, tendono a spostare e separare queste parti..
Legge di Hooke e stress normale
La legge di Hooke afferma che entro i limiti elastici, la sollecitazione normale è direttamente proporzionale alla deformazione subita dalla barra o dall'oggetto. In quel caso:
Sforzo normale ∝ Deformazione dell'unità
Essendo la costante di proporzionalità il modulo di Young (Y):
Sollecitazione normale (σ) = Modulo di Young (Y) x Deformazione unitaria (ε)
σ = Y. ε
Con ε = ΔL / L, dove ΔL è la differenza tra la lunghezza finale e quella iniziale, che è L.
Il modulo di Young o modulo di elasticità è una caratteristica del materiale, le cui dimensioni sono le stesse di quelle di sollecitazione, poiché la deformazione unitaria è adimensionale.
Importanza dello stress nella resistenza dei materiali e geologia
Determinare la resistenza dei materiali alle sollecitazioni è molto importante. Per le strutture utilizzate nella costruzione di edifici, così come nella progettazione di parti per dispositivi diversi, è necessario garantire che i materiali scelti soddisfino adeguatamente la loro funzione.
Per questo motivo, i materiali vengono analizzati in modo esaustivo in laboratorio attraverso test volti a sapere quanta forza possono sopportare prima di deformarsi e rompersi, perdendo così la loro funzione. Sulla base di ciò, si decide se sono idonei o meno a fabbricare una determinata parte o far parte di un dispositivo..
Si ritiene che il primo scienziato a studiare sistematicamente la forza dei materiali sia stato Leonardo Da Vinci. Ha lasciato prove di prove in cui ha determinato la resistenza dei fili appendendo pietre di diverso peso.
Negli sforzi è importante sia l'entità della forza che le dimensioni della struttura e il modo in cui viene applicata, al fine di stabilire i limiti entro i quali il materiale ha un comportamento elastico; cioè, ritorna alla sua forma originale quando lo sforzo cessa.
Con i risultati di questi test, vengono realizzate curve sforzo-deformazione per diversi tipi di materiali, come acciaio, cemento, alluminio e molti altri..
Esempi
I seguenti esempi presumono che le forze siano distribuite uniformemente e che il materiale sia omogeneo e isotropo. Ciò significa che le loro proprietà sono le stesse in entrambe le direzioni. Pertanto è valido applicare l'equazione σ = P / A per trovare le forze.
-Esercizio 1
Nella figura 3 è noto che la sollecitazione normale media che agisce sulla sezione AB ha magnitudo 48 kPa. Trova: a) l'entità della forza F che agisce su CB, b) la tensione sulla sezione BC.
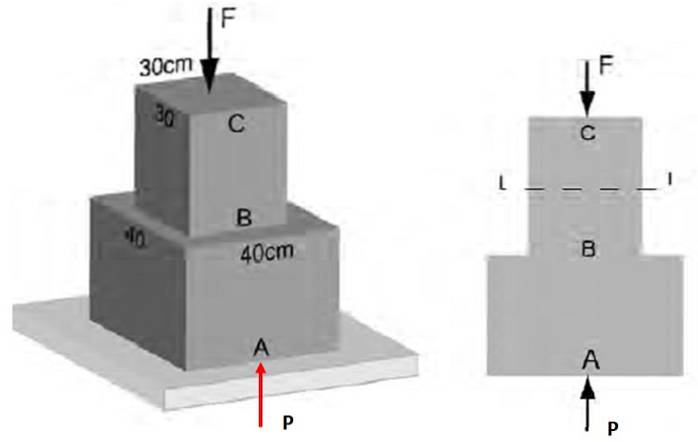
Soluzione
Poiché la struttura è in equilibrio statico, secondo la seconda legge di Newton:
P-F = 0
Lo stress normale sulla sezione AB ha magnitudo:
σAB = P / AAB
Da dove P = σAB . PERAB = 48000 Pa. (40 x 10 -Due m)Due = 7680 N
Quindi F = 7680 N
La sollecitazione normale sulla sezione BC è il quoziente tra la grandezza di F e l'area della sezione trasversale di quel lato:
σAVANTI CRISTO = F / AAVANTI CRISTO = 7680 N / (30 x 10 -Due m)Due = 85,3 kPa.
-Esercizio 2
Un filo di 150 m di lunghezza e 2,5 mm di diametro viene teso con una forza di 500 N. Trova:
a) La tensione longitudinale σ.
b) La deformazione unitaria, sapendo che la lunghezza finale è 150.125 m.
c) Il modulo di elasticità Y di questo filo.
Soluzione
a) σ = F / A = F / π.rDue
Il raggio del filo è la metà del diametro:
r = 1,25 mm = 1,25 x 10-3 m.
L'area della sezione trasversale è π.rDue, allora lo sforzo è:
σ = F / π.rDue = 500 / (π. (1,25 x 10-3)Due Pa = 101859,2 Pa
b) ε = ΔL / L = (Lunghezza finale - Lunghezza iniziale) / Lunghezza iniziale
Perciò:
ε = (150,125 - 150) / 150 = 0,125 / 150 = 0,000833
c) Il modulo di Young del filo si risolve conoscendo i valori di ε e σ calcolati in precedenza:
Y = σ / ε = 101859,2 Pa / 0,000833 = 1,22 x 108 Pa = 122 MPa.
Riferimenti
- Beer, F. 2010. Meccanica dei materiali. 5 °. Edizione. McGraw Hill. 7 - 9.
- Giancoli, D. 2006. Fisica: principi con applicazioni. 6tth Ed. Prentice Hall. 238-242.
- Hibbeler, R.C. 2006. Meccanica dei materiali. 6 °. Edizione. Pearson Education. 22-25
- Valera Negrete, J. 2005. Note sulla fisica generale. UNAM. 87-98.
- Wikipedia. Stress (meccanica). Estratto da: wikipedia.org.



Nessun utente ha ancora commentato questo articolo.