
Prova di tensione come si fa, proprietà, esempi

UN test di resistenza Si tratta di una prova sperimentale che viene eseguita su un campione di materiale per determinare quanto bene resiste alle sollecitazioni di trazione. Grazie ad esso, è possibile conoscere molte delle proprietà meccaniche del materiale e determinare se è appropriato per un particolare progetto..
Il campione è solitamente un cilindro chiamato provetta. Questa è sottoposta ad una tensione, consistente nell'applicare alle estremità due forze opposte che allungano la barra e la deformano. Il test continua esercitando sforzi crescenti, fino a quando il campione si rompe definitivamente.

Notare l'entità delle forze e la deformazione che producono nel provino, dalle piccole forze che non causano deformazioni permanenti, alla sollecitazione che causa la rottura del pezzo..
Qui termina la raccolta dei dati e viene redatto un grafico sforzo-deformazione, che servirà per analizzare il comportamento di materiali come metalli, ceramica, cemento, legno e polimeri..
Indice articolo
- 1 Cosa viene utilizzato per l'esperimento del test di tensione?
- 2 Proprietà e dati ottenuti
- 2.1 Zona elastica
- 2.2 Zona plastica
- 3 Esempi di prove di trazione
- 3.1 Materiali fragili e duttili
- 3.2 Risposta di vari materiali allo stress test
- 4 Riferimenti
Cosa viene utilizzato per l'esperimento del test di tensione?
L'esperimento viene svolto utilizzando macchine speciali come quella mostrata in figura 1, che prevedono lo sforzo necessario per caricare e poi scaricare il materiale per valutarne la deformazione..
Per quanto riguarda il provino, si tratta di un tubo a sezione costante, cilindrico, rettangolare o quadrato, le cui dimensioni sono standardizzate. Le estremità sono più larghe per facilitare il fissaggio al portacampioni, come mostrato nella figura 2 a sinistra.
La lunghezza iniziale Lo La regione calibrata viene misurata e contrassegnata sulla provetta. Viene quindi fissato alla macchina di prova e la macchina di prova inizia..

Proprietà e dati ottenuti
I materiali hanno comportamenti diversi sotto stress, mostrati nel grafico seguente per il quale è stato utilizzato l'acciaio. Le forze applicate sull'asse verticale sono indicate con la lettera greca σ e la deformazione sull'asse orizzontale, chiamata ε.
La deformazione non ha dimensioni, poiché è il quoziente tra la variazione di lunghezza del provino ΔL = LF - Lo e la lunghezza iniziale. A) Sì:
ε = ΔL / Lo
Da parte sua, l'entità della sollecitazione σ è il rapporto forza / area della sezione trasversale.
Nel grafico si distinguono due regioni importanti: zona elastica e zona plastica.
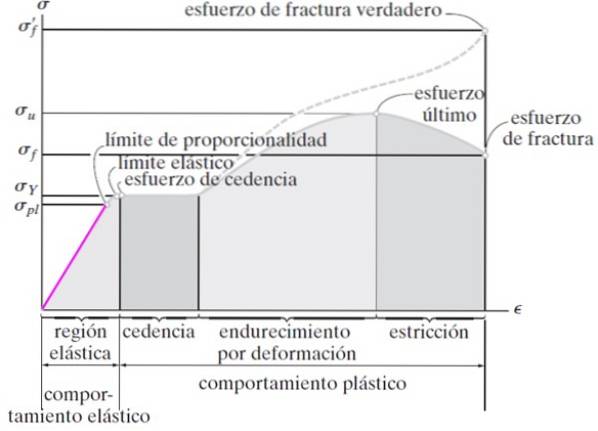
Zona elastica
Quando la tensione di trazione σ è piccola, la deformazione è proporzionale, nota come legge di Hooke:
σ = Y ε
Una volta cessato lo sforzo, il corpo ritorna alle sue dimensioni originali. Questa è la regione elastica a colori nella Figura 3, che si estende fino al punto chiamato limite di proporzionalità. Fino a quel momento il materiale obbedisce alla legge di Hooke.
La costante di proporzionalità Y è la Modulo di Young, caratteristica del materiale e che può essere determinata da prove di trazione e compressione.
Il modulo di Young ha unità di pressione, nel sistema internazionale [Y] = N / m ^ 2 = Pa. La deformazione, come già accennato, è adimensionale, quindi la sollecitazione σ ha anche dimensioni di forza dovute all'unità di area della sezione trasversale e in SI la sua unità sarà il pascal: [σ] = N / m ^ 2 = Pa.
Dal limite di proporzionalità e aumentando lo stress, si avanza in una regione in cui la deformazione è reversibile ma non obbedisce alla legge di Hooke. Termina nel punto da cui il corpo è permanentemente deformato, chiamato limite elastico.
Zona plastica
Il materiale quindi entra nella regione del comportamento plastico. Una volta superata la zona di comportamento elastico, l'acciaio entra nella regione del Cedendo sforzo o creep, in cui il provino si deforma ma non si rompe, sebbene la sollecitazione rimanga costante a σY.
Una volta superata la zona di snervamento, la deformazione aumenta con la sollecitazione applicata, ma non più in modo lineare..
Il materiale subisce modifiche a livello molecolare e si verifica un indurimento. Pertanto vediamo che sono necessari sforzi crescenti per ottenere una deformazione.
Il limite di questa zona è in ultimo sforzo. Il materiale è considerato rotto a questo punto, sebbene l'esemplare sia ancora intero. Da lì, il carico necessario per produrre la deformazione viene ridotto e il provino diventa gradualmente più sottile (stenosi) fino a quando non si rompe (figura 2, a destra).
Questa curva e le sue regioni sono chiamate sollecitazioni da frattura convenzionali. Ma sopra c'è una curva tratteggiata, chiamata vero stress da frattura, che si ottiene registrando la lunghezza istantanea o reale del provino, invece di lavorare con la lunghezza originale per trovare la deformazione, come spiegato all'inizio.
Entrambe le curve, quella vera e quella convenzionale, coincidono nella zona di piccoli sforzi fino alla zona di resa. In ogni caso è previsto che il materiale lavori nel campo elastico per evitare deformazioni permanenti che impediscano il buon funzionamento del manufatto..
Quindi tra i dati più importanti ottenuti dal test c'è lo stress σY che definisce il limite elastico.
Esempi di prove di trazione
Il materiale utilizzato come modello nella descrizione precedente è l'acciaio, ampiamente utilizzato nell'edilizia e nell'industria. Ma ci sono molti materiali come cemento, cemento, vari metalli, leghe e legno, che sono anche ampiamente utilizzati..
Ognuno ha una caratteristica curva sforzo-deformazione e, in base alla sua risposta allo stress o alla trazione, sono classificati in due categorie: fragili o duttili..
Materiali fragili e duttili
Nel grafico seguente σ contro ε (sforzo-deformazione) vengono confrontati materiali fragili (fragile) e duttile (duttile), anche se è necessario chiarire che lo stesso materiale può avere l'una o l'altra risposta a seconda di fattori come la temperatura. I materiali tendono a essere fragili a basse temperature.
La notevole differenza tra i due è che il materiale fragile manca o ha una regione di resa molto piccola. Non appena viene superato il limite elastico, il provino si rompe. D'altra parte, i materiali duttili assorbono più energia prima di rompersi, perché hanno un'ampia zona di plastica.
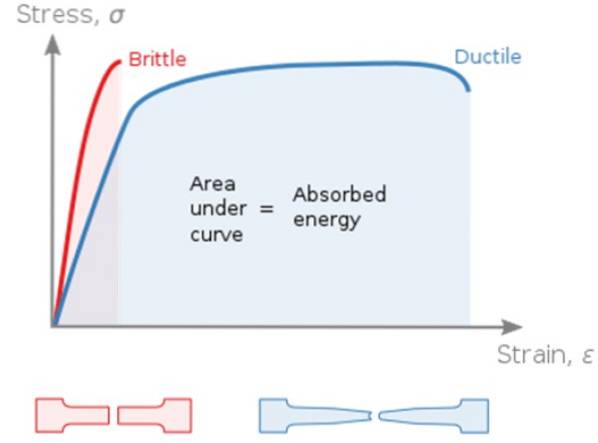
Lo stress test è utile per classificare il materiale, essendo preferibile a seconda dell'applicazione l'uso di materiali duttili, poiché assorbono più energia e sono in grado di deformarsi molto prima della frattura.
Va anche notato che sebbene alcuni materiali siano fragili sotto stress, possono resistere meglio ad altre sollecitazioni, come vedremo di seguito..
Risposta di vari materiali allo stress test
-ghisa grigia: fragile in tensione, più forte in compressione.
-Bronzo: duttile.
-Calcestruzzo: fragile a seconda del tipo di impasto, ma molto resistente alla compressione. Quando sta per essere sottoposto a tensione, necessita di rinforzo mediante barre di acciaio.
-Legna: a seconda dell'origine, è moderatamente duttile.
-Acciaio: fragile se ad alto tenore di carbonio.
-Metacrilato: duttile all'aumentare della temperatura.
Riferimenti
- Beer, F. 2010. Meccanica dei materiali. McGraw Hill. 5 °. Edizione.
- Cavazos, J.L. Meccanica dei materiali. Estratto da: youtube.com.
- Hibbeler, R. 2011. Meccanica dei materiali. Ottava edizione. Pearson.
- Collins, D. Suggerimenti per il movimento lineare. Proprietà meccaniche dei materiali: stress e deformazione. Estratto da: linearmotiontips.com.
- Valera Negrete, J. 2005. Note sulla fisica generale. UNAM.
- Wikipedia. Prova di trazione. Estratto da: es.wikipedia.org.



Nessun utente ha ancora commentato questo articolo.