Il energia potenziale È l'energia che i corpi possiedono in virtù della loro configurazione. Quando gli oggetti interagiscono, ci sono forze tra di loro capaci di fare lavoro, e questa capacità di fare lavoro, che è immagazzinata nella loro disposizione, può essere tradotta in energia..
Ad esempio, gli esseri umani hanno sfruttato l'energia potenziale delle cascate da tempo immemorabile, prima dalle filature e poi dalle centrali idroelettriche..
D'altra parte, molti materiali hanno una notevole capacità di lavorare deformandosi e poi tornando alla loro dimensione originale. E in altre circostanze, la disposizione della carica elettrica consente l'immagazzinamento di energia potenziale elettrica, come ad esempio in un condensatore.
L'energia potenziale offre molte possibilità per essere trasformata in altre forme di energia utilizzabile, da qui l'importanza di conoscere le leggi che la governano..
Indice articolo
L'energia potenziale di un oggetto ha la sua origine nelle forze che lo influenzano. Tuttavia, l'energia potenziale è una grandezza scalare, mentre le forze sono vettoriali. Pertanto, per specificare l'energia potenziale, è sufficiente indicarne il valore numerico e le unità selezionate.
Un'altra qualità importante è il tipo di forza con cui l'energia potenziale può essere immagazzinata, poiché non tutte le forze hanno questa virtù. Solo le forze conservatrici immagazzinano energia potenziale nei sistemi su cui agiscono.
Una forza conservatrice è quella per la quale il lavoro non dipende dal percorso seguito dall'oggetto, ma solo dal punto di partenza e dal punto di arrivo. La forza che guida l'acqua che cade è la gravità, che è una forza conservatrice.
D'altra parte, anche le forze elastiche ed elettrostatiche hanno questa qualità, quindi c'è un'energia potenziale ad esse associata..
Le forze che non soddisfano il suddetto requisito sono chiamate non conservatrici; esempio di loro sono in attrito e resistenza all'aria.
Poiché l'energia potenziale deriva sempre da forze conservatrici come quelle già menzionate, parliamo di energia potenziale gravitazionale, energia potenziale elastica, energia potenziale elettrostatica, energia potenziale nucleare e energia potenziale chimica..
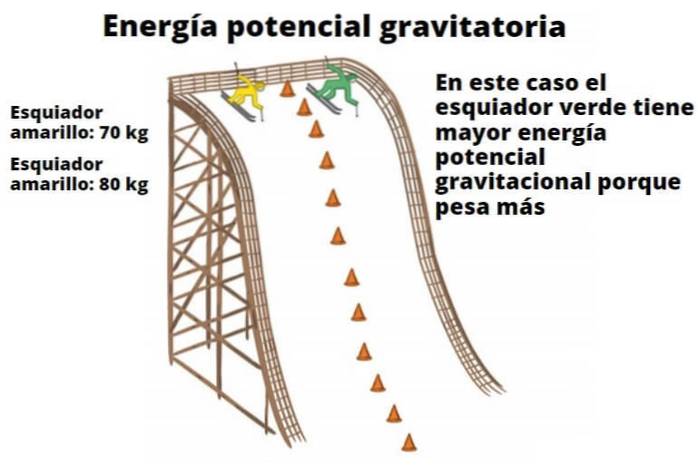
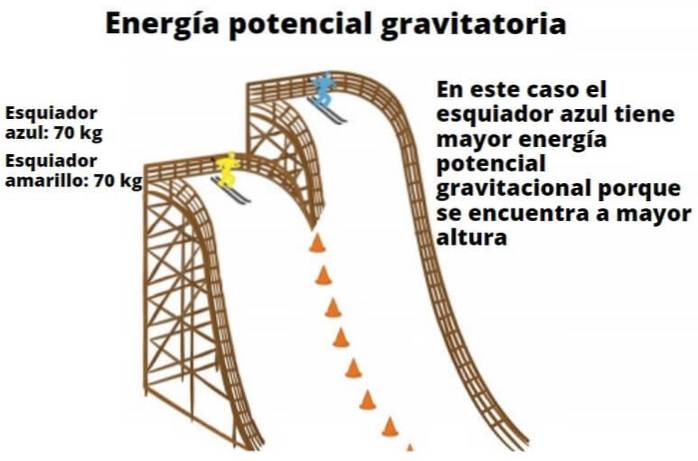
Ogni oggetto ha energia potenziale in funzione della sua altezza dal suolo. Questo fatto apparentemente semplice illustra perché l'acqua che cade è in grado di azionare le turbine e alla fine di essere trasformata in energia elettrica. L'esempio degli sciatori mostrato qui mostra anche la relazione tra peso e altezza rispetto all'energia potenziale gravitazionale.
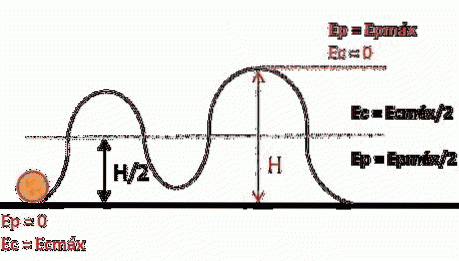
Un altro esempio è quello di un'auto sulle montagne russe, che ha un'energia potenziale maggiore quando si trova a una certa altezza dal suolo. Una volta raggiunto il livello del suolo, la sua altezza è pari a zero e tutta la sua energia potenziale è stata trasformata in energia cinetica (energia di movimento).
Oggetti come molle, archi, balestre ed elastici sono in grado di immagazzinare energia potenziale elastica..
L'elasticità di un corpo o di un materiale è descritta dalla legge di Hooke (fino a certi limiti), la quale ci dice che la forza capace di esercitare quando viene compressa o stirata è proporzionale alla sua deformazione.
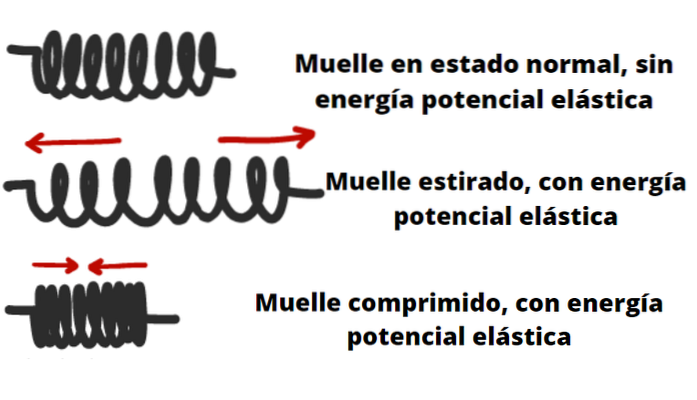
Ad esempio nel caso di una molla o di una molla, ciò significa che più si restringe o si allunga, maggiore è la forza che può esercitare su un oggetto posto ad un'estremità..
È l'energia che hanno le cariche elettriche in virtù della loro configurazione. Le cariche elettriche dello stesso segno si respingono a vicenda, quindi per posizionare una coppia di cariche positive - o negative - in una determinata posizione, deve funzionare un agente esterno. Altrimenti tenderebbero a separarsi.
Questo lavoro viene archiviato nel modo in cui sono stati posizionati i carichi. Più le cariche dello stesso segno sono vicine, maggiore sarà l'energia potenziale che avrà la configurazione. L'opposto accade quando si tratta di un sacco di segni diversi; come si attraggono, più sono vicini, minore è l'energia potenziale che hanno.
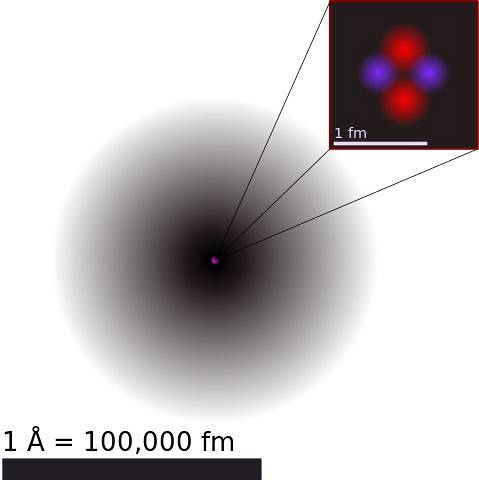
Il nucleo atomico è costituito da protoni e neutroni, chiamati genericamente nucleoni. I primi hanno una carica elettrica positiva e i secondi sono neutri..
Poiché sono agglomerati in uno spazio minuscolo oltre l'immaginazione, e sapendo che cariche dello stesso segno si respingono, ci si chiede come il nucleo atomico rimanga coeso.
La risposta sta in forze diverse dalla repulsione elettrostatica, tipiche del nucleo, come l'interazione nucleare forte e l'interazione nucleare debole. Queste sono forze molto forti, che superano di gran lunga la forza elettrostatica.
Questa forma di energia potenziale deriva da come sono disposti gli atomi e le molecole delle sostanze, secondo i diversi tipi di legami chimici..
Quando si verifica una reazione chimica, questa energia può essere trasformata in altri tipi, ad esempio tramite una batteria o una batteria elettrica.
L'energia potenziale è presente nella vita quotidiana in molti modi. Osservarne gli effetti è facile come posizionare un oggetto a una certa altezza ed essere certi che possa rotolare o cadere in qualsiasi momento.
Ecco alcune manifestazioni dei tipi di energia potenziale precedentemente descritti:
-Montagne russe
-Macchine o palle che rotolano in discesa
-Archi e frecce
-Batterie elettriche
-Un orologio a pendolo
-Oscillare su un'altalena
-Salta su un trampolino
-Utilizzando una penna retrattile.
Vedi: esempi di energia potenziale.
L'energia potenziale dipende dal lavoro svolto dalla forza e questo a sua volta non dipende dalla traiettoria, quindi si può affermare che:
-Se A e B sono due punti, il lavoro WAB necessario per andare da A a B è uguale al lavoro necessario per andare da B ad A. Pertanto: WAB = WBA, così:
WAB + WBA = 0
-E se si provano due diverse traiettorie 1 e 2 per unire detti punti A e B, anche il lavoro svolto in entrambi i casi è lo stesso:
W1 = WDue.
In entrambi i casi l'oggetto subisce un cambiamento nell'energia potenziale:
Variazione = Energia potenziale finale - Energia potenziale iniziale
ΔU = Ufinale - Oiniziale = UB - OPER
Ebbene, l'energia potenziale dell'oggetto è definita come il negativo del lavoro svolto dalla forza (conservativa):
ΔU = -WAB
Ma poiché il lavoro è definito da questo integrale:
Nota che le unità di energia potenziale sono le stesse di quelle di lavoro. Nel Sistema Internazionale SI l'unità è il joule, che è abbreviato J ed è equivalente a 1 newton x metro, dal fisico inglese James Joule (1818-1889).
Altre unità di energia includono cgs erg, libbra-forza x piede, BTU (British Thermal Unit), calorie e chilowattora.
Vediamo di seguito alcuni casi particolari di come calcolare l'energia potenziale.
In prossimità della superficie terrestre, la forza di gravità punta verticalmente verso il basso e la sua grandezza è data dall'equazione Peso = massa x gravità.
Denotando l'asse verticale con la lettera "y" e assegnando a questa direzione il vettore unitario j, positivo su e negativo verso il basso, il cambiamento di energia potenziale quando un corpo si muove da y = yPER fino a y = yB è:
U (y) = mgy
La legge di Hooke ci dice che la forza è proporzionale alla deformazione:
F = -k.x
Qui X è la deformazione e K è una costante autovettura della molla, che indica quanto sia rigida. Attraverso questa espressione viene calcolata l'energia potenziale elastica, tenendo conto di ciò io è il vettore unitario nella direzione orizzontale:
U (x) = ½ kxDue
Quando hai una carica elettrica puntiforme Q, produce un campo elettrico che percepisce un'altra carica puntiforme che cosa, e che funziona su di esso quando viene spostato da una posizione all'altra al centro del campo. La forza elettrostatica tra due cariche puntiformi ha una direzione radiale, simboleggiata dal vettore unitario r:
Una primavera la cui costante è K = 10,0 N / cm inizialmente si estende per 1,00 cm dalla sua lunghezza di equilibrio. Viene richiesto di calcolare l'energia aggiuntiva necessaria per allungare la molla fino a 5,00 cm oltre la sua lunghezza di equilibrio..
Sostituendo direttamente x = 1.00 cm nell'equazione per U (x), otteniamo N.cm, ma i centimetri devono essere convertiti in metri per ottenere l'energia in joule:
U (1) = 0,5 x 10,0 N / cm x (1,00 cm)Due = 5 N. cm = 0,05 J; U (5) = 0,5 x 10,0 N / cm x (5,00 cm)Due = 125 N.cm = 1,25 J
Pertanto la differenza di energia ricercata è 1,25 - 0,05 J = 1,20 J..
Un piccolo blocco viene rilasciato da fermo dal punto A, per scorrere lungo la rampa curva priva di attrito fino al punto B. Da lì entra in una lunga superficie orizzontale ruvida, con un coefficiente di attrito dinamico μK = 0,2. Trova quanto lontano dal punto B si ferma, supponendo che hPER= 3 m.
Quando il blocco è ad un'altezza hPER Rispetto al suolo, ha energia potenziale gravitazionale a causa della sua altezza. Quando viene rilasciata, questa energia potenziale viene gradualmente convertita in energia cinetica e mentre scivola lungo la rampa curva liscia, la sua velocità aumenta..
Durante il percorso da A a B, le equazioni del moto rettilineo variato in modo uniforme non possono essere applicate. Sebbene la gravità sia responsabile del movimento del blocco, il movimento che sperimenta è più complesso, perché la traiettoria non è rettilinea.
Tuttavia, poiché la gravità è una forza conservativa e non c'è attrito sulla rampa, è possibile utilizzare la conservazione dell'energia meccanica per trovare la velocità alla fine della rampa:
Energia meccanica in A = Energia meccanica in B
m.g.hPER + ½ m.vPERDue = m.g.hB + ½ m.vBDue
L'espressione è semplificata notando che la massa appare in ogni termine. Viene rilasciato da rest vPER = 0. E hB è a livello del suolo, hB = 0. Con queste semplificazioni, l'espressione si riduce a:
vBDue = ghPER
Ora il blocco inizia il suo percorso nel tratto accidentato con questa velocità e infine si ferma al punto C. Pertanto vC = 0. L'energia meccanica non viene più conservata, perché l'attrito è una forza dissipativa, che ha fatto lavorare sul blocco dato da:
Wtoccare = - forza di attrito x distanza percorsa
Questo lavoro ha un segno negativo, poiché l'attrito cinetico rallenta l'oggetto, contrastandone il movimento. L'entità dell'attrito cinetico FK è:
FK = μK .N
Dove N è l'ampiezza della forza normale. La forza normale è esercitata dalla superficie sul blocco e poiché la superficie è completamente orizzontale, bilancia il peso P = mg, quindi l'entità della normale è:
N = mg
Che porta a:
FK = μK .mg
Il lavoro che FK fa circa il blocco è: WK = - fK .D = - μK .mg.D.
Questo lavoro è equivalente a cambiamento di energia meccanica, calcolato in questo modo:
Energia meccanica in C - Energia meccanica in B =
ΔEm = (UC +KC)- (OB + KB) = - μK .mg.D
In questa equazione ci sono alcuni termini che svaniscono: KC = 0, poiché il blocco si ferma in C e anche U svanisconoC = UB, perché questi punti sono a livello del suolo. La semplificazione si traduce in:
- KB = - μK .m.g.D
½ m.vBDue = μK .m.g.D
La massa si annulla nuovamente e D può essere ottenuto come segue:
D = (½ vBDue) / (μK . g) = (½ vBDue) / (μK . g) = (½g.hPER) / (μK . g) = (½ hPER) / μK = 0,5 x 3 m / 0,2 = 7,5 m
Nessun utente ha ancora commentato questo articolo.