
Dinamica di un sistema di particelle esempi, esercizi
Il dinamica di un sistema particellare Consiste nell'applicazione delle leggi del moto di Newton a un insieme di particelle, che possono essere discrete (le particelle possono essere contate) o far parte di un oggetto esteso, in questo caso il sistema è continuo.
Per spiegare il moto di un sistema di particelle, è scomodo analizzarle separatamente e vedere quali forze agiscono su di essa. Viene invece definito un punto rappresentativo dell'insieme, chiamato Centro di massa.
Descrivere il moto del centro di massa offre una panoramica molto accurata del moto complessivo dell'insieme, permette anche di applicare le leggi di Newton in modo analogo a quando l'oggetto è considerato come una particella adimensionale.
Quest'ultimo modello, chiamato modello di particelle, È utile per descrivere le traduzioni e anche quando non è necessario considerare le dimensioni dell'oggetto. Ma gli oggetti ordinari hanno dimensioni e se hanno anche movimento rotatorio, è necessario tenere conto dei punti su cui vengono applicate le forze.
Indice articolo
- 1 Esempi
- 1.1 La Terra e la Luna
- 1.2 Oggetti estesi
- 2 Il centro di massa di un sistema di particelle
- Movimento da 2,1 cm
- 2.2 Forza su CM
- 3 Esercizio risolto
- 3.1 Soluzione a
- 3.2 Soluzione b
- 3.3 Soluzione c
- 4 Riferimenti
Esempi
La Terra e la Luna

Un insieme di particelle discrete m1, mDue, m3... che alla fine si sposta rispetto all'origine di un sistema di coordinate, a causa di una forza risultante che agisce su di esse, è un buon esempio di un sistema di particelle.
La Terra può essere considerata come una particella e la Luna un'altra, quindi entrambe costituiscono un sistema di 2 particelle sotto l'azione della forza di gravità del Sole..
Oggetti estesi
Una persona, un animale o qualsiasi oggetto nell'ambiente può anche essere considerato come un sistema di particelle, solo che queste sono così piccole da non poter essere contate una per una. Questo è un sistema continuo, ma tenendo conto di alcune considerazioni, il suo trattamento è lo stesso di un sistema discreto.
Di seguito sono riportati i dettagli.
Il centro di massa di un sistema di particelle
Per iniziare lo studio di un sistema particellare, dobbiamo trovare il centro di massa (CM), che è il punto in cui è concentrata tutta la massa del sistema..
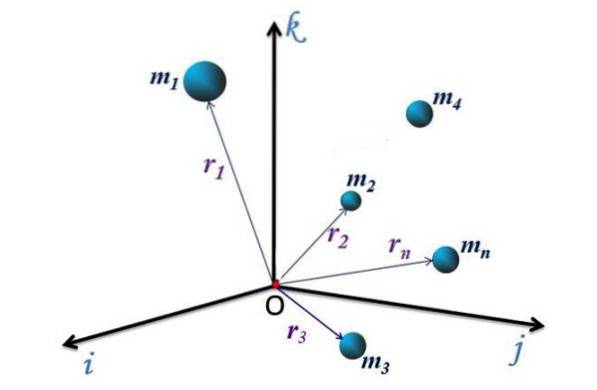
Per il sistema discreto della Figura 1, con n particelle, ciascuna ha un vettore di posizione diretto dall'origine O del sistema di coordinate al punto P (x, y, z) dove si trova la particella. Questi vettori sono indicati come r1, rDue, r3... rn.
Le coordinate del CM vengono calcolate utilizzando le seguenti equazioni:

Dove ciascuna delle masse dell'insieme è rappresentata come m1, mDue, m3... mn. Notare che la somma ∑ mio è uguale alla massa totale M dell'assieme. Se il sistema è continuo, le somme vengono sostituite con integrali.
Ciascuna delle direzioni perpendicolari è rappresentata dai vettori unitari io, j Y K, quindi, il vettore di posizione del CM, indicato rCM, può essere espresso da:
rCM = xCM io + YCM j + zCM K
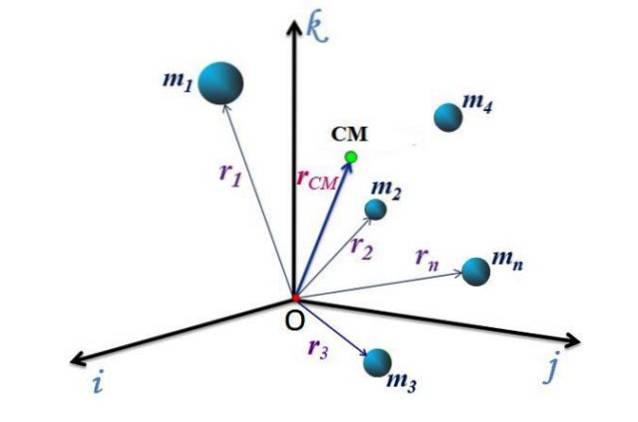
Movimento CM
Una volta che la posizione del centro di massa è nota, si applicano le equazioni del moto note. La velocità del CM è la prima derivata della posizione rispetto al tempo:

In questo caso, il sistema ha uno slancio totale P che è calcolato come il prodotto della massa totale del sistema e la velocità del centro di massa:
P = M ∙vCM
In alternativa, la quantità di moto totale del sistema può essere calcolata direttamente:
P = m1v1 + mDuevDue + m3v3 +…. = ∑ mio vio
Mentre l'accelerazione del CM è la derivata della velocità:

Forza su CM
Le forze che agiscono su un sistema di particelle possono essere:
- Forze interne, dovute alle interazioni tra le stesse particelle.
- Forze esterne, causate da agenti esterni al sistema.
Poiché le forze interne sono presentate a coppie, di uguale grandezza e direzione, ma direzioni opposte, secondo la terza legge di Newton, è vero che:
∑ Fint = 0
Pertanto, le forze interne non alterano il movimento del tutto, ma sono molto importanti per determinare l'energia interna..
Se il sistema è isolato e non ci sono forze esterne, secondo la prima legge di Newton il centro di massa è fermo o si muove con moto rettilineo uniforme. Altrimenti, il centro di massa subisce un'accelerazione data da:
∑ Fext = M ∙perCM
Dove M è la massa totale del sistema. L'equazione sopra può essere scritta in questo modo:

E significa che la forza esterna è equivalente alla variazione temporale della quantità di moto, un altro modo di esprimere la seconda legge di Newton e la stessa che il famoso fisico inglese usò nel suo libro Principio.
Esercizio risolto
Il centro di massa di un sistema a 2 particelle si trova sull'asse x in un certo momento, nella posizione x = 2,0 me si muove con una velocità di 5,0 m / s nella stessa direzione e in una direzione positiva. Se una delle particelle è all'origine e l'altra, di massa 0,1 kg, è a riposo a x = 8,0 m, calcolare:
a) La massa della particella che è all'origine.
b) Quantità di movimento del sistema
c) Qual è la velocità della particella all'origine?
Soluzione a
Dall'equazione per la posizione del centro di massa:
rCM = xCM io + YCM j + zCM k = 2,0 m io
Poiché il CM ha solo una coordinata x, viene utilizzata solo la prima equazione del trio fornita in precedenza:

Ora le coordinate vengono sostituite, se la particella all'origine è indicata come numero 1 e l'altra come numero 2, i dati numerici sono:
X1 = 0 m, xDue = 8,0 m, mDue = 0,1 kg, xCM = 2,0 m
Rimanente:

Soluzione b
La quantità di movimento del sistema è calcolata da:
P = M ∙vCM
La massa totale M è uguale a:
M = 0,3 kg + 0,1 kg = 0,4 kg
Perciò:
P = 0,4 kg ∙ 5,0 m / s io = 2 kg.m / s io
Soluzione c
Dall'equazione per P di un sistema a due particelle, si cancella v1, poiché gli altri dati sono noti, poiché l'affermazione dice che la particella 2 è a riposo, quindi:
vDue = 0
Y P sembra semplicemente:
P = m1v1
v1 = P / m1 = 2 kg.m / s io / 0,3 kg = 6,67 m / s io
Riferimenti
- Duke University. Sistemi di particelle. Recupero da: webhome.phy.duke.edu.
- Rex, A. 2011. Fondamenti di fisica. Pearson.
- Sears, Zemansky. 2016. Fisica universitaria con fisica moderna. 14th. Ed. Volume 1. Pearson.
- Serway, R., Jewett, J. (2008). Fisica per la scienza e l'ingegneria. Volume 1. 7th. Ed. Cengage Learning.
- Tipler, P. (2006) Physics for Science and Technology. 5a Ed. Volume 1. Editoriale Reverté.



Nessun utente ha ancora commentato questo articolo.