
Diagramma del corpo libero come farlo, esempi, esercizio
UN Diagramma di corpo libero, diagramma del corpo isolato o diagramma delle forze, è un diagramma in cui le forze che agiscono su un corpo sono rappresentate da frecce.
Assicurati di includere nel diagramma tutti le forze che agiscono sull'oggetto, e poiché è una quantità vettoriale, la freccia ha il compito di indicarne la direzione e il senso, mentre la sua lunghezza fornisce un'idea del modulo o dell'intensità.
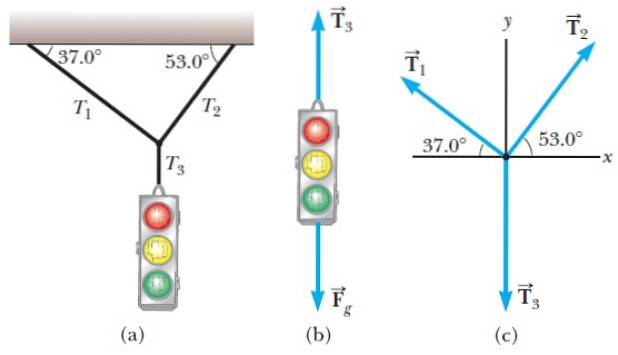
Nella figura 1 abbiamo un esempio di diagramma a corpo libero che andremo ad analizzare.
La situazione è la seguente: un semaforo sospeso a riposo da alcuni cavi (figura 1a). Su di essa agiscono due forze, una è quella esercitata dalla Terra, che è il peso. Nel diagramma è indicato come Fg e agisce verticalmente verso il basso.
L'altra forza è la tensione nella corda verticale, chiamata T3 e che va in direzione verticale verso l'alto, trattenendo il semaforo e impedendogli di cadere a terra.
Quando un problema ha più di un oggetto, è necessario disegnare un diagramma per ciascuno separatamente..
Il nodo tra le funi inclinate e la fune che trattiene il semaforo è considerato un oggetto puntuale e il suo diagramma a corpo libero è in Figura 1c. Nota che per il nodo, la tensione T3 è diretto verso il basso.
È importante notare che le forze esercitate dall'oggetto su altri corpi non dovrebbero apparire nel diagramma del corpo libero, ma solo quelli che agiscono su di esso.
Indice articolo
- 1 Esempi di diagramma a corpo libero
- 1.1 Una persona che tira un baule o un container
- 1.2 Un blocco che scorre lungo un piano inclinato
- 1.3 La macchina di Atwood
- 2 Esercizio risolto
- 2.1 Soluzione
- 3 Riferimenti
Esempi di diagrammi a corpo libero
Il diagramma del corpo libero permette l'applicazione delle leggi di Newton e con esse determina lo stato di moto o di riposo dell'oggetto su cui agiscono le forze. Nel caso del semaforo rappresentato, possiamo determinare il valore delle tensioni nei cavi che trattengono il semaforo, conoscendo il peso di questo.
Una volta conosciuti questi dati, vengono selezionati cavi adatti per appendere il semaforo e che assolvono alla loro funzione senza collassare.
I diagrammi a corpo libero sono usati per descrivere varie situazioni quotidiane, come queste:
Una persona che tira un baule o un container
È molto comune per le persone dover trasportare oggetti pesanti come il contenitore nella figura. Per fare questo devono esercitare una forza F sul contenitore, che in questo esempio è orizzontale e a destra, che è la direzione del movimento.
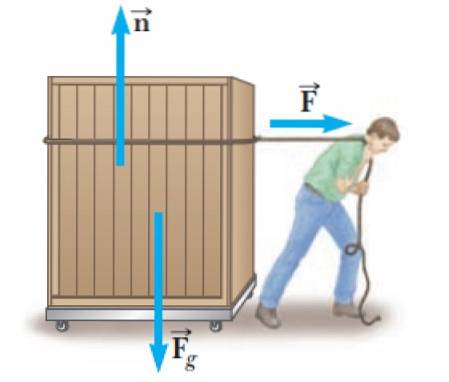
Ma questa non è l'unica forza che agisce su di lui, c'è anche la normalità n, esercitato dalla superficie piana della piattaforma con ruote. E infine c'è il suo peso: Fg, diretto verticalmente verso il basso.
La normale è una forza che nasce ogni volta che due superfici sono in contatto ed è sempre perpendicolare alla superficie che la esercita. In questo caso, la piattaforma su ruote esercita una normale pressione sul contenitore.
Un blocco che scorre lungo un piano inclinato
Alcune scrivanie hanno il tavolo leggermente inclinato per rendere più facile prendere appunti e leggere. Ha anche una fessura portapenne, ma tutti abbiamo messo la matita sul tavolo fuori dalla fessura e abbiamo visto come scivola sul tavolo.
Quali forze agiscono sulla matita?
Gli stessi che agiscono sul blocco mostrato nel seguente diagramma a corpo libero:
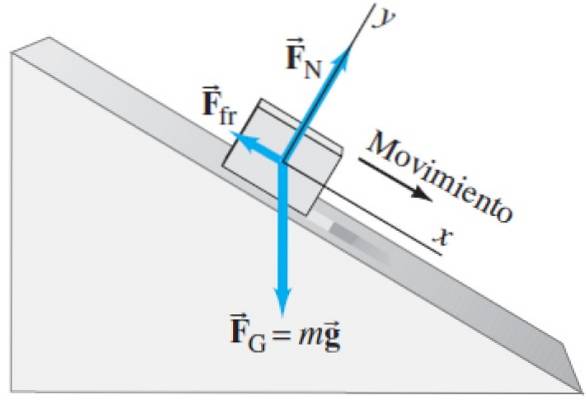
Il normale FN è la forza che la superficie del tavolo esercita sulla matita o sul blocco supportato. A differenza dell'esempio precedente, la normale non è verticale, ma inclinata. Ricorda che la normale è la forza che il tavolo esercita sul blocco ed è perpendicolare ad esso. Poiché il tavolo è inclinato, anche quello normale.
Come sempre il peso Fg è verticale, indipendentemente dall'inclinazione del sistema.
E finalmente abbiamo una nuova forza che agisce, che è l'attrito cinetico Ffr tra il tavolo e la matita o il blocco. Anche l'attrito è una forza di contatto, ma a differenza del normale, è una forza tangenziale (parallela) alla superficie. Nota anche che è sempre diretto nella direzione opposta al movimento..
La macchina di Atwood
La macchina Atwood è una macchina semplice che consiste in una puleggia leggera e priva di attrito sulla rotaia, attraverso la quale passa una fune leggera e inestensibile.
Vi sono appesi due oggetti di massa m1 e mDue. Quando uno degli oggetti sale, l'altro scende, come mostrato in figura 4a:
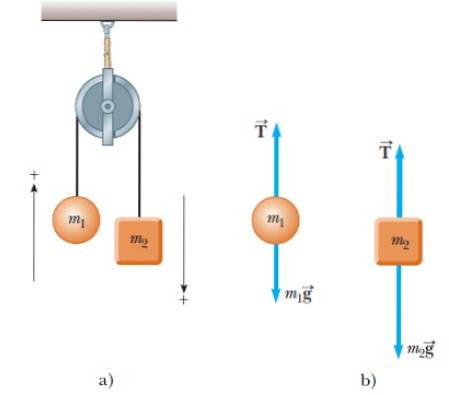
Poiché ci sono due oggetti, per ognuno viene creato un diagramma a corpo libero separatamente. Per entrambi gli oggetti ci sono solo due forze: la tensione nella corda T e i rispettivi pesi.
Nella figura, ogni peso è espresso direttamente come prodotto di massa e accelerazione. Da parte sua, la tensione è sempre diretta verticalmente lungo la fune in tensione.
Esercizio risolto
Applicare le leggi di Newton per determinare l'accelerazione con cui le masse si muovono dalla macchina Atwood mostrata nella sezione precedente.
Soluzione
La seconda legge di Newton afferma che la somma delle forze è uguale al prodotto della massa e dell'accelerazione.
La convenzione del segno in ogni massa può essere diversa, quindi prenderemo il movimento in senso positivo, come indicato nel grafico, la prima massa sale e la seconda scende.
In alcuni problemi l'affermazione non fornisce informazioni, quindi i segni devono essere assegnati arbitrariamente e se il risultato dell'accelerazione è negativo, il sistema di massa si muove nella direzione opposta a quella inizialmente ipotizzata.
-Per massa 1 (aumento):
T - m1g = m1per
-Per massa 2 (bassa):
-T + mDueg = mDueper
Entrambe le equazioni formano un sistema di equazioni lineari di due incognite, poiché la tensione appare con un segno diverso in ogni equazione, le aggiungiamo semplicemente termine per termine e la tensione annulla:
mDueg - m1g = m1a + mDueper
a = mDueg - m1g / (m1 + mDue)
Riferimenti
- Bauer, W. 2011. Fisica per l'ingegneria e le scienze. Volume 1. Mc Graw Hill.
- Giancoli, D. 2006. Fisica: principi con applicazioni. 6 °. Ed prentice hall.
- Serway, R., Vulle, C. 2011. College Physics. 9 ° Ed. Cengage Learning.
- Tipler, P. (2006) Physics for Science and Technology. 5a Ed. Volume 1. Editoriale Reverté.
- Tippens, P. 2011. Fisica: concetti e applicazioni. 7a edizione. Mcgraw hill


Nessun utente ha ancora commentato questo articolo.