
Qual è la differenza tra percorso e spostamento?
Il differenza principale tra traiettoria e spostamento è che la seconda è la distanza e la direzione percorsa da un oggetto, mentre la prima è il percorso o la forma che prende il movimento di quell'oggetto.
Tuttavia, per vedere più chiaramente le differenze tra spostamento e traiettoria, è meglio specificarne la concettualizzazione attraverso esempi che consentono una migliore comprensione di entrambi i termini..
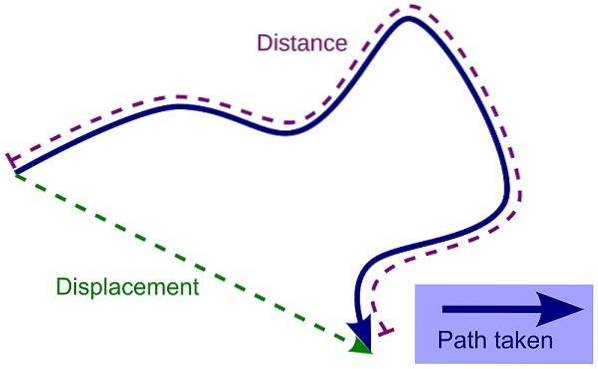
Dislocamento
Si intende la distanza e la direzione percorsa da un oggetto tenendo conto della sua posizione iniziale e della sua posizione finale, sempre in linea retta. Per il suo calcolo, trattandosi di una grandezza vettoriale, vengono utilizzate le misure di lunghezza note come centimetri, metri o chilometri..
La formula per calcolare lo spostamento è definita come segue:
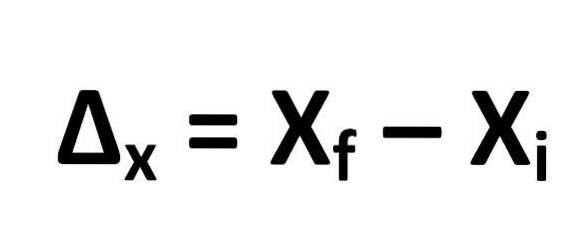
Da cui ne consegue che:
- ΔX = cilindrata
- XF = posizione finale dell'oggetto
- Xio = posizione iniziale dell'oggetto
Esempio di spostamento
1- Se un gruppo di bambini si trova all'inizio di un percorso, la cui posizione iniziale è di 50m, si muove in linea retta, determinare lo spostamento in ciascuno dei punti XF .
- XF = 120 m
- XF = 90 m
- XF = 60 m
- XF = 40 m
2- I dati del problema vengono estratti sostituendo i valori di XDue e X1 nella formula offset:
- ΔX = ?
- Xio = 50 m
- ΔX = XF - Xio
- ΔX = 120 m - 50 m = 70 m
3- In questo primo approccio diciamo che ΔX è uguale a 120m, che corrisponde al primo valore che troviamo di XF, meno 50 m che è il valore di Xio, Il risultato è 70 m, cioè quando si raggiungono i 120 m percorsi, lo spostamento era di 70 m a destra.
4- Procediamo a risolvere allo stesso modo per i valori di b, c e d
- ΔX = 90 m - 50 m = 40 m
- ΔX = 60 m - 50 m = 10 m
- ΔX = 40 m - 50 m = - 10 m
In questo caso, lo spostamento ci ha dato negativo, ciò significa che la posizione finale è nella direzione opposta alla posizione iniziale.
Traiettoria
È il percorso o la linea determinata da un oggetto durante il suo movimento e la sua valutazione nel Sistema Internazionale, generalmente adotta forme geometriche come la linea, la parabola, il cerchio o l'ellisse). Si identifica tramite una linea immaginaria e poiché è una quantità scalare si misura in metri.
Va notato che per calcolare la traiettoria dobbiamo sapere se il corpo è a riposo o in movimento, cioè è sottoposto al sistema di riferimento che selezioniamo.
L'equazione per calcolare la traiettoria di un oggetto nel Sistema Internazionale è data da:
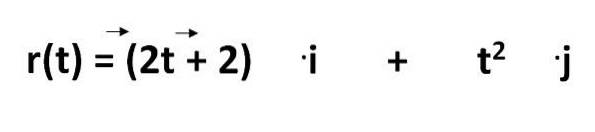
Di cui dobbiamo:
- r (t) = è l'equazione del cammino
- 2t - 2 e tDue = rappresenta le coordinate in funzione del tempo
- .Io e .j = sono i vettori unitari
Per comprendere il calcolo del percorso percorso da un oggetto, svilupperemo il seguente esempio:
- Calcola l'equazione delle traiettorie dei seguenti vettori di posizione:
- r (t) = (2t + 7) .i + tDue .j
- r (t) = (t - 2) .i + 2t .j
Primo passo: poiché un'equazione del percorso è una funzione di X, per fare ciò definire i valori di X e Y rispettivamente in ciascuno dei vettori proposti:
1- Risolvi il primo vettore di posizione:
- r (t) = (2t + 7) .i + tDue .j
2- Ty = f (x), dove X è dato dal contenuto del vettore unitario .i e Y è dato dal contenuto del vettore unitario .j:
- X = 2t + 7
- Y = tDue
3- y = f (x), cioè il tempo non fa parte dell'espressione quindi dobbiamo risolverlo, abbiamo:
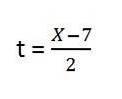
4- Sostituiamo il gioco in Y. Rimane:
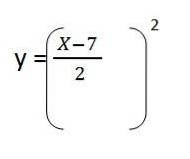
5- Risolviamo il contenuto delle parentesi e abbiamo l'equazione del percorso risultante per il primo vettore unitario:
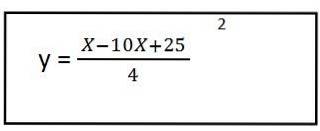
Come possiamo vedere, ci ha dato un'equazione di secondo grado, questo significa che la traiettoria ha la forma di una parabola.
Secondo passo: procediamo allo stesso modo per calcolare la traiettoria del secondo vettore unitario
r (t) = (t - 2) .i + 2t .j
- X = t - 2
- Y = 2t
2- Seguendo i passaggi che abbiamo visto in precedenza y = f (x), dobbiamo azzerare il tempo perché non fa parte dell'espressione, ci rimane:
- t = X + 2
3- Sostituiamo il gioco in Y, rimanendo:
- y = 2 (X + 2)
4- Risolvendo le parentesi abbiamo l'equazione della traiettoria risultante per il secondo vettore unitario:
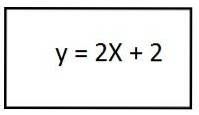
In questa procedura, il risultato era una linea retta, che ci dice che la traiettoria ha una forma rettilinea.
Una volta compresi i concetti di spostamento e traiettoria, possiamo dedurre il resto delle differenze che esistono tra entrambi i termini.
Più differenze tra spostamento e traiettoria
Dislocamento
- È la distanza e la direzione percorsa da un oggetto tenendo conto della sua posizione iniziale e della sua posizione finale.
- Succede sempre in linea retta.
- Si riconosce con una freccia.
- Usa misurazioni della lunghezza (centimetri, metri, chilometri).
- È una quantità vettoriale.
- Prendi in considerazione la direzione percorsa (a destra oa sinistra)
- Non considera il tempo trascorso durante il tour.
- Non dipende da un sistema di riferimento.
- Quando il punto iniziale è lo stesso punto iniziale, l'offset è zero.
- Il modulo deve coincidere con lo spazio da percorrere purché il percorso sia una linea retta e non ci siano cambi di direzione da seguire.
- Il modulo tende ad aumentare o diminuire man mano che si verifica il movimento, tenendo presente la traiettoria.
Traiettoria
È il percorso o la linea determinata da un oggetto durante il suo movimento. Adotta forme geometriche (diritte, paraboliche, circolari o ellittiche).
- È rappresentato da una linea immaginaria.
- Si misura in metri.
- È una quantità scalare.
- Non tiene conto della direzione percorsa.
- Considera il tempo trascorso durante il tour.
- Dipende da un sistema di riferimento.
- Quando il punto di partenza o la posizione iniziale è uguale alla posizione finale, la traiettoria è data dalla distanza percorsa.
- Il valore della traiettoria coincide con il modulo del vettore di spostamento, se la traiettoria risultante è una linea retta, ma non ci sono cambiamenti nella direzione da seguire.
- Aumenta sempre quando il corpo si muove, indipendentemente dalla traiettoria.
Riferimenti
- Alvarado, N. (1972) Fisico. Primo anno di scienze. Editoriale Fotoprin C.A. Venezuela.
- Fernández, M; Fidalgo, J. (2016). Fisica e Chimica 1 ° Baccalaureato. Edizioni Paraninfo, S.A. Spagna.
- Istituto guatemalteco di educazione radiofonica. (2011) Fisica fondamentale. Primo semestre del gruppo Zaculeu. Guatemala.
- Fernández, P. (2014) Campo scientifico-tecnologico. Edizioni Paraninfo. S.A. Spagna.
- Fisica Lab (2015) Vector Displacement. Estratto da: fisicalab.com.
- Esempi di. (2013) Displacement. Estratto da: examplesde.com.
- Living Room Home Project (2014) Cos'è lo spostamento? Estratto da: salonhogar.net.
- Laboratorio di fisica (2015) Concetto di traiettoria ed equazione di posizione. Estratto da: fisicalab.com.


Nessun utente ha ancora commentato questo articolo.