
Formule di conduttanza, calcoli, esempi, esercizi
Il conduttanza di un conduttore è definita come la struttura che deve far passare la corrente elettrica. Dipende non solo dal materiale utilizzato per la sua fabbricazione, ma anche dalla sua geometria: lunghezza e area della sezione trasversale.
Il simbolo utilizzato per la conduttanza è G, ed è l'inverso della resistenza elettrica R, una quantità leggermente più familiare. L'unità del Sistema Internazionale SI per la conduttanza è l'inverso dell'ohm, indicato come Ω-1 e riceve il nome di siemens (S).

Altri termini usati nell'elettricità che suonano simili alla conduttanza e sono correlati sono conducibilità e il guida, ma non dovrebbero essere confusi. Il primo di questi termini è una proprietà intrinseca della sostanza con cui è realizzato il conduttore e il secondo descrive il flusso di carica elettrica attraverso di esso..
Per un conduttore elettrico con area della sezione trasversale costante PER, lunghezza L e conducibilità σ, la conduttanza è data da:
G = σ.A / L
Maggiore è la conduttività, maggiore è la conduttanza. Inoltre, maggiore è l'area della sezione trasversale, più facile è per il conduttore passare la corrente. Al contrario, maggiore è la lunghezza L, minore è la conduttanza, poiché i portatori di corrente perdono più energia su percorsi più lunghi..
Indice articolo
- 1 Come viene calcolata la conduttanza?
- 1.1 Unità di conduttanza
- 2 esempi
- 2.1 Conduttività e conduttanza
- 2.2 Resistenze in parallelo
- 3 esercizi
- 3.1 - Esercizio 1
- 3.2 - Esercizio 2
- 4 Riferimenti
Come viene calcolata la conduttanza?
La conduttanza G per un conduttore con area della sezione trasversale costante viene calcolata secondo l'equazione data sopra. Questo è importante, perché se la sezione trasversale non è costante, è necessario utilizzare il calcolo integrale per trovare sia la resistenza che la conduttanza.
Poiché è l'inverso della resistenza, la conduttanza G può essere calcolata sapendo che:
G = 1 / R
La resistenza elettrica di un conduttore, infatti, può essere misurata direttamente con un multimetro, un dispositivo che misura anche corrente e tensione..
Unità di conduttanza
Come affermato all'inizio, l'unità di conduttanza nel sistema internazionale è la Siemens (S). Si dice che un conduttore abbia una conduttanza di 1 S se la corrente che lo attraversa aumenta di 1 ampere per ogni volt di differenza di potenziale.
Vediamo come ciò sia possibile attraverso la legge di Ohm, se è scritta in termini di conduttanza:
V = I.R = I / G
Dove V è la differenza di tensione o potenziale tra le estremità del conduttore e io intensità di corrente. In termini di queste grandezze, la formula è simile a questa:
G = I / V
In precedenza l'unità per la conduttanza era il mho (ohm scritto al contrario) indicato come Ʊ, che è un omega maiuscolo invertito. Questa notazione è stata deprecata ed è stata sostituita dal siemens in onore dell'ingegnere e inventore tedesco Ernst Von Siemens (1816-1892), pioniere delle telecomunicazioni, ma entrambi sono totalmente equivalenti.
1 mho = 1 siemens = 1 A / V (ampere / volt)
In altri sistemi di misurazione il statsiemens (statS) (nel sistema cgs o centimetro-grammo-secondo) e il absiemens (abS) (sistema cgs elettromagnetico) con la "s" alla fine, senza indicare singolare o plurale, poiché derivano da un nome proprio.
Alcune equivalenze
1 statS = 1,11265 x 10 -12 siemens
1 abS = 1 x 109 siemens
Esempi
Come accennato prima, avendo la resistenza, la conduttanza è immediatamente nota quando si determina il valore inverso o reciproco. In questo modo una resistenza elettrica di 100 ohm è equivalente a 0,01 siemens, per esempio.
Ecco altri due esempi di utilizzo della conduttanza:
Conduttività e conduttanza
Sono termini diversi, come già indicato. La conduttività è una proprietà della sostanza con cui è realizzato il conduttore, mentre la conduttanza è propria del conduttore.
La conducibilità può essere espressa in termini di G come:
σ = G. (L / A)
Ecco una tabella con le conduttività dei materiali conduttivi usati di frequente:
Tabella 1. Conduttività, resistività e coefficiente termico di alcuni conduttori. Temperatura di riferimento: 20 ºC.
| Metallo | σ x 106 (Voi) | ρ x 10-8 (Ω.m) | α ºC-1 |
|---|---|---|---|
| Argento | 62.9 | 1.59 | 0.0058 |
| Rame | 56.5 | 1.77 | 0.0038 |
| Oro | 41.0 | 2.44 | 0.0034 |
| Alluminio | 35.4 | 2.82 | 0.0039 |
| Tungsteno | 18.0 | 5.60 | 0.0045 |
| Ferro | 10.0 | 10.0 | 0.0050 |
Resistori in parallelo
Quando si hanno circuiti con resistenze in parallelo, a volte è necessario ottenere la resistenza equivalente. Conoscere il valore della resistenza equivalente consente di sostituire un unico valore per l'insieme di resistenze.
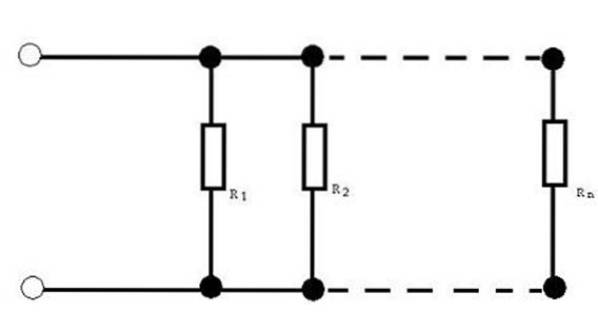
Per questa configurazione del resistore, la resistenza equivalente è data da:
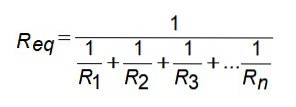
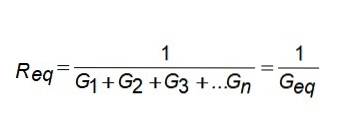
Geq = G1 + GDue + G3 +... Gn
Cioè, la conduttanza equivalente è la somma delle conduttanze. Se vuoi conoscere la resistenza equivalente, inverti semplicemente il risultato.
Formazione
- Esercizio 1
a) Scrivi la legge di Ohm in termini di conduttanza.
b) Trovare la conduttanza di un filo di tungsteno di 5,4 cm di lunghezza e 0,15 mm di diametro.
c) Ora una corrente di 1,5 A viene fatta passare attraverso il filo. Qual è la potenziale differenza tra le estremità di questo conduttore?
Soluzione a
Dalle sezioni precedenti devi:
V = I / G
G = σ.A / L
Sostituendo quest'ultimo nel primo, assomiglia a questo:
V = I /(σ.A/L) = I.L / σ.A
Dove:
-Io è l'intensità della corrente.
-L è la lunghezza del conduttore.
-σ è la conducibilità.
-A è l'area della sezione trasversale.
Soluzione b
Per calcolare la conduttanza di questo filo di tungsteno, è necessaria la sua conduttività, che si trova nella Tabella 1:
σ = 18 x106 Voi
L = 5,4 cm = 5,4 x 10-Due m
D = 0,15 mm = 0,15 x 10-3 m
A = π.DDue / 4 = π. (0,15 x 10-3 m)Due / 4 = 1,77 x 10-8 mDue
Sostituendo nell'equazione abbiamo:
G = σ.A / L = 18 x106 Ye. 1,77 x 10-8 mDue / 0,15 x 10-3 m = 2120,6 S.
Soluzione c
V = I / G = 1,5 A / 2120,6 S = 0,71 mV.
- Esercizio 2
Trova la resistenza equivalente nel seguente circuito e sapendo che io = 2 A, calcola iX e la potenza dissipata dal circuito:
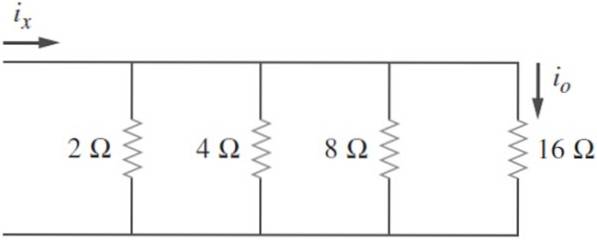
Soluzione
Le resistenze sono elencate: R1= 2 Ω; RDue= 4 Ω; R3= 8 Ω; R4= 16 Ω
Quindi la conduttanza viene calcolata in ogni caso: G1 = 0,5 Ʊ; GDue = 0,25 Ʊ; G3 = 0,125 Ʊ; G4 = 0,0625 Ʊ
E infine vengono aggiunti come indicato prima, per trovare la conduttanza equivalente:
Geq = G1 + GDue + G3 +... Gn = 0,5 Ʊ + 0,25 Ʊ + 0,125 Ʊ + 0,0625 Ʊ = 0,9375 Ʊ
Pertanto Req = 1,07 Ω.
La tensione ai capi di R4 è V4 = io. R4 = 2 A. 16 Ω = 32 V, ed è lo stesso per tutti i resistori, poiché sono collegati in parallelo. Quindi è possibile trovare le correnti che fluiscono attraverso ciascuna resistenza:
-io1 = V1 / R1 = 32 V / 2 Ω = 16 A
-ioDue = VDue / RDue = 32 V / 4 Ω = 8 A
-io3 = V3 / R3 = 32 V / 8 Ω = 4 A
-ioX = i1 + ioDue + io3 + ioo = 16 + 8 + 4 + 2 A = 30 A
Infine, la potenza dissipata P è:
P = (iX)Due. Req = 30 A x 1,07 Ω = 32,1 W.
Riferimenti
- Alexander, C. 2006. Fondamenti di circuiti elettrici. 3 °. Edizione. Mcgraw hill.
- Conversione megaampere / millivolt in absiemens Calculator. Estratto da: pinkbird.org.
- García, L. 2014. Elettromagnetismo. 2 °. Edizione. Università industriale di Santander. Colombia.
- Knight, R. 2017. Physics for Scientists and Engineering: a Strategy Approach. Pearson.
- Roller, D. 1990. Fisica. Elettricità, magnetismo e ottica. Volume II. Reverté editoriale.
- Wikipedia. Conduttanza elettrica. Estratto da: es.wikipedia.org.
- Wikipedia. Siemens. Estratto da: es.wikipedia.org.



Nessun utente ha ancora commentato questo articolo.