Il accelerazione istantanea È il cambiamento che la velocità subisce per unità di tempo in ogni istante del movimento. Nel momento preciso in cui il "dragster”L'immagine è stata fotografata, ha subito un'accelerazione di 29,4 m / sDue. Ciò significa che in quel momento la sua velocità veniva aumentata di 29,4 m / s nell'arco di 1 s. Ciò equivale a 105 km / h in appena 1 secondo.
Una competizione di dragster è facilmente modellabile assumendo che l'auto da corsa sia un oggetto puntuale. P che si muove in linea retta. Su questa linea viene scelto un asse orientato con l'origine O che chiameremo asseBUE) o solo asse X.
Le variabili cinematiche che definiscono e descrivono il movimento sono:
Sono tutte quantità vettoriali. Quindi hanno una grandezza, una direzione e un senso.
Nel caso di moto rettilineo ci sono solo due possibili direzioni: positiva (+) nella direzione di (BUE) o negativo (-) nella direzione opposta di (BUE). Pertanto, è possibile fare a meno della notazione vettoriale formale e utilizzare i segni per indicare il senso della grandezza.
Indice articolo
Supponiamo che nell'istante t la particella ha velocità v (t) e nell'istante t ' la sua velocità è v (t ').
Quindi il cambiamento che la velocità ha avuto in quel periodo di tempo è stato Δv = v (t ') - v (t). Da qui l'accelerazione nel lasso di tempo Δt = t '- t , sarebbe dato dal quoziente:
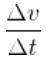
Questo quoziente è l'accelerazione media am nel periodo di tempo Δt tra gli istanti t e t '.
Se volessimo calcolare l'accelerazione proprio all'istante t, allora t 'dovrebbe essere una quantità non significativamente maggiore di t. Con questo Δt, che è la differenza tra i due, dovrebbe essere quasi zero.
Matematicamente si indica come segue: Δt → 0 e si ottiene:
IO) Una particella si muove lungo l'asse X con velocità costante v0 = 3 m / s. Quale sarà l'accelerazione della particella?
La derivata di una costante è zero, quindi l'accelerazione di una particella che si muove con velocità costante è zero.
II) Una particella si muove sull'asse X e la sua velocità cambia nel tempo secondo la seguente formula:
v (t) = 2 - 3t
Dove la velocità è misurata in m / se il tempo in s. Quale sarà l'accelerazione della particella?
)
Il risultato è interpretato in questo modo: per ogni istante l'accelerazione è di -3 m / s.
Tra gli istanti 0 se 2/3 s la velocità è positiva mentre l'accelerazione è negativa, cioè in quell'intervallo la particella diminuisce o decelera.
All'istante 2/3 s la sua velocità diventa zero, ma siccome permane un'accelerazione di -3 m / s, da quell'istante la velocità si inverte (diventa negativa).
Negli istanti dopo ⅔ s, la particella accelera, poiché ogni volta che la sua velocità diventa più negativa, cioè la sua velocità (modulo di velocità) cresce.
III) La figura mostra una curva che rappresenta la velocità in funzione del tempo, per una particella che si muove lungo l'asse X. Trova il segno dell'accelerazione agli istanti t1, tDue e tu3. Indicare anche se la particella sta accelerando o decelerando.
L'accelerazione è la derivata della funzione velocità, quindi è equivalente alla pendenza della tangente alla curva v (t) per un dato istante t.
Per l'istante t1, la pendenza è negativa, quindi l'accelerazione è negativa. E poiché in quell'istante la velocità è positiva, possiamo affermare che in quell'istante la particella sta decelerando.
Per l'istante tDue la tangente alla curva v (t) è orizzontale, quindi la sua pendenza è zero. Il cellulare ha accelerazione zero, quindi a tDue la particella non accelera né decelera.
Per l'istante t3, la pendenza della tangente alla curva v (t) è positiva. Con un'accelerazione positiva la particella sta realmente accelerando, perché in quel momento anche la velocità è positiva.
Nella sezione precedente, l'accelerazione istantanea è stata definita dalla velocità istantanea. In altre parole, se la velocità è nota in ogni istante, allora è anche possibile conoscere l'accelerazione in ogni istante del movimento..
È possibile il processo inverso. Cioè, conoscendo l'accelerazione per ogni istante, è possibile calcolare la velocità istantanea.
Se l'operazione che permette di passare dalla velocità all'accelerazione è la derivata, l'operazione matematica opposta è l'integrazione.
L'accelerazione di una particella che si muove lungo l'asse X è a (t) = ¼ tDue. Dove t è misurato in secondi e a in m / s. Determina l'accelerazione e la velocità della particella a 2 s di moto, sapendo che nell'istante iniziale t0 = 0 era a riposo.
A 2 s l'accelerazione è di 1 m / sDue e la velocità per l'istante t sarà data da:
Un oggetto si muove lungo l'asse X con una velocità in m / s, data da:
v (t) = 3 tDue - 2 t, dove t è misurato in secondi. Determina l'accelerazione a volte: 0s, 1s, 3s.
Prendendo la derivata di v (t) rispetto at, si ottiene l'accelerazione in qualsiasi istante:
a (t) = 6t -2
Allora a (0) = -2 m / sDue ; a (1) = 4 m / sDue ; a (3) = 16 m / sDue .
Una sfera di metallo viene rilasciata dalla cima di un edificio. L'accelerazione di caduta è l'accelerazione di gravità che può essere approssimata dal valore 10 m / s2 e rivolta verso il basso. Determina la velocità della sfera 3 s dopo che è stata rilasciata.
Questo problema riguarda l'accelerazione di gravità. Prendendo la direzione verticale come positiva giù, abbiamo che l'accelerazione della sfera è:
a (t) = 10 m / sDue
E la velocità sarà data da:
Una sfera di metallo viene lanciata verso l'alto con una velocità iniziale di 30 m / s. L'accelerazione del moto è l'accelerazione di gravità che può essere approssimata dal valore 10 m / sDue e rivolto verso il basso. Determina la velocità della sfera a 2 se 4 s dopo che è stata colpita.
La direzione verticale sarà considerata positiva verso l'alto. EIn tal caso l'accelerazione del moto sarà data da
a (t) = -10 m / sDue
La velocità in funzione del tempo sarà data da:
Dopo 4 s dallo sparo, la velocità sarà 30 - 10 ∙ 4 = -10 m / s. Il che significa che a 4 s la sfera sta discendendo con una velocità di 10 m / s.
Nessun utente ha ancora commentato questo articolo.