Il accelerazione di gravità o l'accelerazione gravitazionale è definita come l'intensità del campo gravitazionale della Terra. Cioè, la forza che esercita su qualsiasi oggetto, per unità di massa.
È indicato dall'ormai familiare lettera g e il suo valore approssimativo in prossimità della superficie terrestre è 9,8 m / sDue. Questo valore può subire piccole variazioni con la latitudine geografica e anche con l'altezza rispetto al livello del mare..
L'accelerazione di gravità, oltre ad avere la suddetta magnitudine, ha direzione e senso. In effetti, è diretto verticalmente verso il centro della terra.
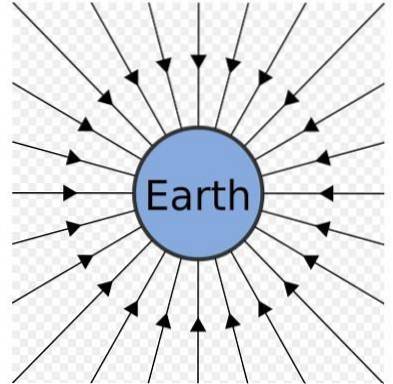
Il campo gravitazionale della Terra può essere rappresentato come un insieme di linee radiali che puntano verso il centro, come mostrato nella figura precedente.
Indice articolo
Il valore dell'accelerazione di gravità sulla Terra o su qualsiasi altro pianeta è equivalente all'intensità del campo gravitazionale che produce, che non dipende dagli oggetti che la circondano, ma solo dalla propria massa e raggio..
L'accelerazione di gravità è spesso definita come l'accelerazione subita da qualsiasi oggetto in caduta libera in prossimità della superficie terrestre..
In pratica questo è ciò che accade quasi sempre, come vedremo nelle sezioni seguenti, in cui verrà utilizzata la Legge di Gravitazione Universale di Newton..
Si dice che Newton abbia scoperto questa famosa legge mentre meditava sulla caduta dei corpi sotto un albero. Quando ha sentito il colpo della mela in testa, ha capito subito che la forza che fa cadere la mela è la stessa che fa orbitare la Luna intorno alla Terra.
Che la leggenda della mela fosse vera o meno, Newton si rese conto che l'entità della forza gravitazionale di attrazione tra due oggetti qualsiasi, ad esempio tra la Terra e la Luna, o la Terra e la mela, deve dipendere dalle loro masse.:
La forza gravitazionale è sempre attraente; cioè, i due corpi che colpisce si attraggono. Il contrario non è possibile, poiché le orbite dei corpi celesti sono chiuse o aperte (comete, ad esempio) e una forza repulsiva non può mai produrre un'orbita chiusa. Quindi le masse si attraggono sempre, non importa cosa.
Un'approssimazione abbastanza buona alla vera forma della Terra (m1) E della Luna o della mela (mDue) è presumere che abbiano una forma sferica. La figura seguente è una rappresentazione di questo fenomeno.
Qui sia la forza esercitata da m1 Circa mDue, come quello che mDue Circa m1, entrambi di uguale grandezza e diretti lungo la linea che unisce i centri. Non vengono cancellati, poiché vengono applicati a oggetti diversi.
In tutte le sezioni successive si assume che gli oggetti siano omogenei e sferici, quindi il loro baricentro coincide con il loro centro geometrico. Si può presumere che tutta la massa si sia concentrata proprio lì.
La gravità può essere misurata con un gravimetro, un dispositivo di misurazione della gravità utilizzato nei rilievi gravimetrici geofisici. Attualmente sono molto più sofisticati degli originali, ma all'inizio erano basati sul pendolo.
Il pendolo è costituito da una corda sottile, leggera e inestensibile di lunghezza L. Una delle sue estremità è fissata ad un supporto e dall'altra è appesa una massa m..
Quando il sistema è in equilibrio, la massa è sospesa verticalmente, ma quando se ne separa inizia ad oscillare, eseguendo un movimento avanti e indietro. La gravità ne è responsabile. Per tutto ciò che segue, è valido supporre che la gravità sia l'unica forza che agisce sul pendolo.
Il periodo T di oscillazione del pendolo per piccole oscillazioni è dato dalla seguente equazione:
- 1 sfera di metallo.
- Corda di diverse lunghezze, almeno 5.
- Nastro di misurazione.
- Trasportatore.
- Cronometro.
- Una staffa per fissare il pendolo.
- Carta millimetrata o programma per computer con foglio di calcolo.
Il valore standard di gravità sulla Terra è: 9,81 m / sDue, a 45º di latitudine nord e al livello del mare. Poiché la Terra non è una sfera perfetta, i valori di g variare leggermente, essendo più alto ai poli e più basso all'equatore.
Chi vuole conoscere il valore nella propria località lo può trovare aggiornato sul sito web dell'Istituto tedesco di metrologia PTB (Physikalisch-Technische Bundesanstalt), nella sezione Sistema informativo gravitazionale (GESSO).
Il campo gravitazionale della Luna è stato determinato analizzando i segnali radio delle sonde spaziali in orbita attorno al satellite. Il suo valore sulla superficie lunare è di 1,62 m / sDue
Il valore di gP per un pianeta dipende dalla sua massa M e dal suo raggio R come segue:
Perciò:
Per il pianeta Marte sono disponibili i seguenti dati:
M = 6,4185 x 102. 3 kg
R = 3390 km
G = 6,67 x 10-undici N.mDue/ kgDue
Con questi dati sappiamo che la gravità di Marte è di 3,71 m / sDue. Naturalmente, la stessa equazione può essere applicata con i dati della Luna o di qualsiasi altro pianeta e quindi stimare il valore della sua gravità.
Supponiamo che sia la Terra che una mela siano di forma sferica. La massa della Terra è M = 5,98 x 1024 kg e il suo raggio è R = 6,37 x 106 m. La massa della mela è m = 0,10 kg. Supponiamo che non ci sia altra forza all'infuori della gravità. Dalla Legge di Gravitazione Universale di Newton trova:
a) La forza gravitazionale che la Terra esercita sulla mela.
b) L'accelerazione subita dalla mela quando viene rilasciata da una certa altezza, secondo la Seconda Legge di Newton.
a) La mela (presumibilmente sferica, come la Terra) ha un raggio molto piccolo rispetto al raggio della Terra ed è immersa nel suo campo gravitazionale. La figura seguente ovviamente non è in scala, ma c'è un diagramma del campo gravitazionale g, e la forza F esercitato dalla terra sulla mela:
Applicando la Legge di Gravitazione Universale di Newton, la distanza tra i centri può essere considerata all'incirca lo stesso valore del raggio terrestre (anche l'altezza da cui cade la mela è trascurabile rispetto al raggio terrestre). Perciò:
b) Secondo la seconda legge di Newton, l'entità della forza esercitata sulla mela è:
F = ma = mg
Il cui valore è 0,983 N, secondo il calcolo precedente. Uguagliando entrambi i valori e quindi risolvendo per l'entità dell'accelerazione, otteniamo:
mg = 0,983 N
g = 0,983 N / 0,10 kg = 9,83 m / sDue
Questa è un'ottima approssimazione del valore standard di gravità.
Nessun utente ha ancora commentato questo articolo.