Il accelerazione centripeta perc, Chiamato anche radiale o normale, è l'accelerazione che un oggetto in movimento trasporta quando descrive un percorso circolare. La sua grandezza è vDue/ r, dove r è il raggio del cerchio, è diretto verso il centro di esso ed è responsabile di mantenere il cellulare in movimento.
Le dimensioni dell'accelerazione centripeta sono la lunghezza per unità di tempo al quadrato. Nel Sistema Internazionale sono m / sDue. Se per qualche motivo scompare l'accelerazione centripeta, lo stesso accade alla forza che costringe il mobile a mantenere il percorso circolare.
Questo è ciò che accade a un'auto che cerca di curvare su una pista piana e ghiacciata, dove l'attrito tra il terreno e le ruote è insufficiente perché l'auto possa curvare. Quindi l'unica possibilità che rimane è quella di muoversi in linea retta ed è per questo che esce dalla curva.
Indice articolo
Quando un oggetto si muove in cerchio, in ogni momento l'accelerazione centripeta è diretta radialmente verso il centro della circonferenza, direzione che è perpendicolare al percorso seguito.
Poiché la velocità è sempre tangente al percorso, la velocità e l'accelerazione centripeta risultano essere perpendicolari. Quindi velocità e accelerazione non hanno sempre la stessa direzione.
In queste circostanze, il cellulare ha la possibilità di descrivere la circonferenza con velocità costante o variabile. Il primo caso è noto come Movimento circolare uniforme o MCU per il suo acronimo, il secondo caso sarà un movimento circolare variabile.
In entrambi i casi, l'accelerazione centripeta è responsabile di mantenere il mobile in rotazione, assicurando che la velocità vari solo in direzione e in direzione.
Tuttavia, per avere un Moto Circolare Variabile, sarebbe necessaria un'altra componente dell'accelerazione nella stessa direzione della velocità, che ha il compito di aumentare o diminuire la velocità. Questo componente dell'accelerazione è noto come accelerazione tangenziale.
Il movimento circolare variabile e il movimento curvilineo in generale hanno entrambe le componenti dell'accelerazione, perché il movimento curvilineo può essere immaginato come il percorso attraverso innumerevoli archi circonferenziali che compongono il percorso curvo..
Ora, una forza è responsabile di fornire l'accelerazione. Per un satellite in orbita attorno alla terra, è la forza di gravità. E poiché la gravità agisce sempre perpendicolare alla traiettoria, non altera la velocità del satellite..
In tal caso la gravità agisce come un forza centripeta, che non è una classe di forza speciale o separata, ma quella che, nel caso del satellite, è diretta radialmente verso il centro della terra.
In altri tipi di movimento circolare, ad esempio un'auto che svolta in curva, il ruolo della forza centripeta è svolto dall'attrito statico e per una pietra legata ad una fune che viene ruotata in circolo, la tensione nella fune è la forza che forza il mobile per girare.
L'accelerazione centripeta è calcolata dall'espressione:
ac = vDue/ r
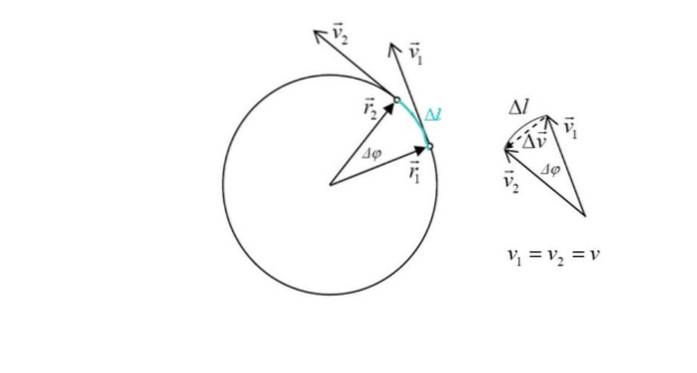
Questa espressione verrà derivata di seguito. Per definizione, l'accelerazione è il cambiamento di velocità nel tempo:
Il cellulare impiega un po 'di tempo Δt nel percorso, che è piccolo, poiché i punti sono molto vicini.
La figura mostra anche due vettori di posizione r1 Y rDue, il cui modulo è lo stesso: il raggio r della circonferenza. L'angolo tra i due punti è Δφ. In verde evidenzia il arco attraversato dal mobile, indicato come Δl.
Nella figura a destra si vede che l'ampiezza di Δv, la variazione di velocità è approssimativamente proporzionale a Δl, poiché l'angolo Δφ è piccolo. Ma il cambiamento di velocità è precisamente correlato all'accelerazione. Dal triangolo si può vedere, aggiungendo i vettori che:
v1 + Δv = vDue → Δv = vDue - v1
Δv è interessante, poiché è proporzionale all'accelerazione centripeta. Dalla figura si può vedere che poiché l'angolo Δφ è piccolo, il vettore Δv è essenzialmente perpendicolare a entrambi v1 piace vDue e indica il centro della circonferenza.
Sebbene fino ad ora i vettori siano evidenziati in grassetto, per gli effetti di natura geometrica che seguono, lavoriamo con i moduli o le grandezze di questi vettori, facendo a meno della notazione vettoriale.
Qualcos'altro: è necessario utilizzare la definizione di angolo centrale, che è:
Δφ= Δl / r
Ora vengono confrontate entrambe le cifre, che sono proporzionali rispetto all'angolo Δφ è comune:
Dividendo per Δt:
perc= vDue/ r
Una particella si muove in un cerchio di raggio 2,70 m. In un dato momento la sua accelerazione è di 1,05 m / sDue in una direzione che forma un angolo di 32,0º con la direzione del movimento. Calcola la tua velocità:
a) In quel momento
b) 2,00 secondi dopo, ipotizzando un'accelerazione tangenziale costante.
È un movimento circolare vario, poiché l'affermazione indica che l'accelerazione ha un dato angolo con la direzione del movimento che non è né 0º (non potrebbe essere un movimento circolare) né 90º (sarebbe un movimento circolare uniforme).
Pertanto le due componenti -radiale e tangenziale- coesistono. Saranno indicati come ac giàt e sono disegnati nella figura seguente. Il vettore in verde è il vettore di accelerazione netta o semplicemente accelerazione per.
perc = a.cos θ = 1,05 m / sDue . cos 32,0º = 0,89 m / sDue (in rosso)
pert = a.sen θ = 1,05 m / sDue . sin 32,0º = 0,57 m / sDue (in arancione)
Dac = vDue/ r, poi:
v = vo +pert. t = 1,6 m / s + (0,57 x 2) m / s = 2,74 m / s
Nessun utente ha ancora commentato questo articolo.